Puntos y vectores.
Sistema de referencia euclídeo u ortonormal
Puntos y vectores
Dado un punto cualquiera A del plano y un vector cualquiera, existe un único representante de dicho vector con origen en A . De esta manera, si definimos O como un origen de coordenadas, tenemos que:

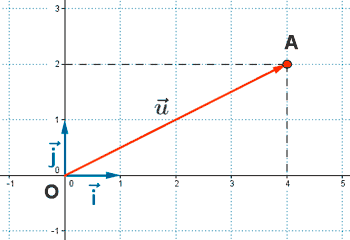
Sistema de referencia euclídeo u ortonormal

Coordenadas de vectores en un sistema de referencia euclideo

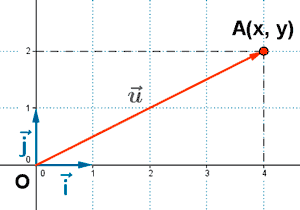

Módulo del vector AB y distancia entre dos puntos
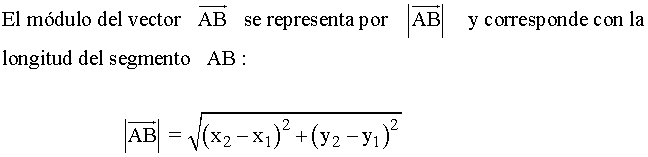
DISTANCIA ENTRE DOS PUNTOS:
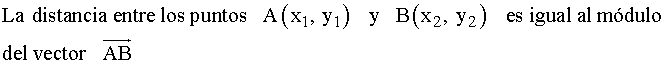
![]()
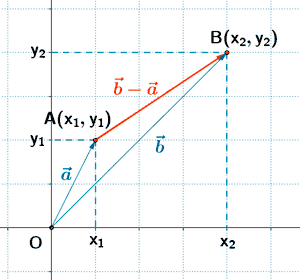
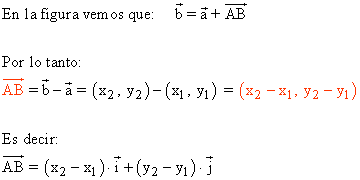
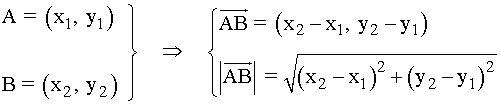
Ejemplo:
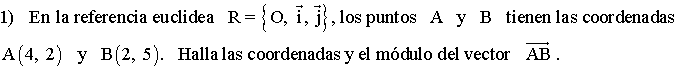
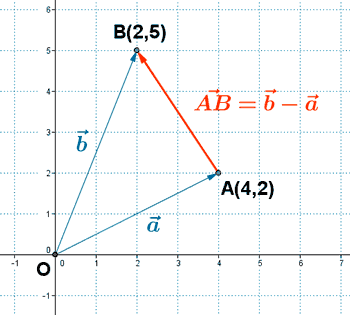
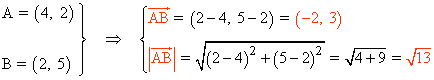

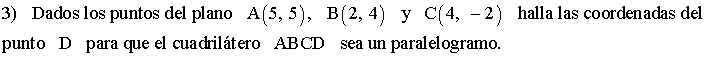
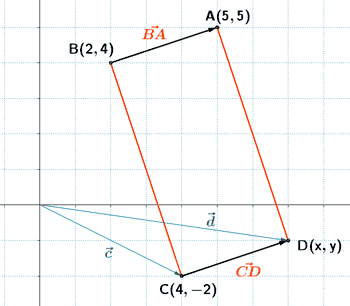

Punto medio de un segmento
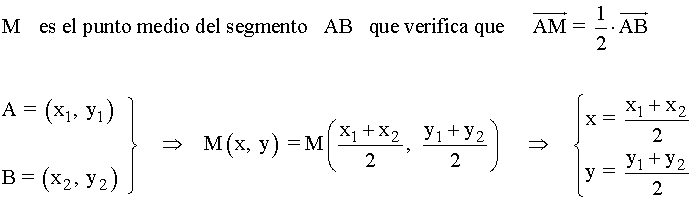
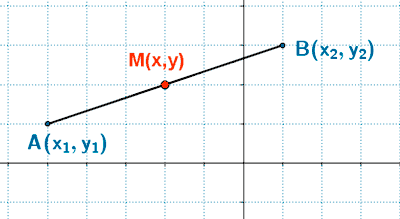
Ejemplo:
Dados los puntos A(-5, 1) y B(1, 3) , calcula el punto medio del segmento AB .
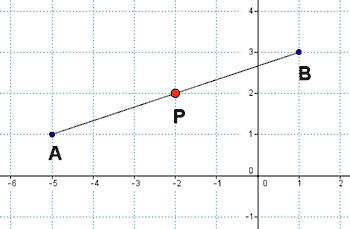

División de un segmento en n partes iguales
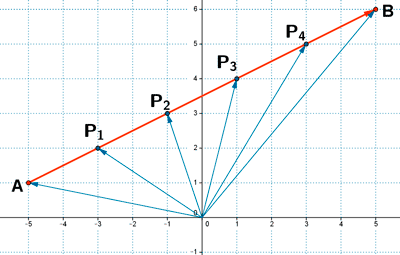
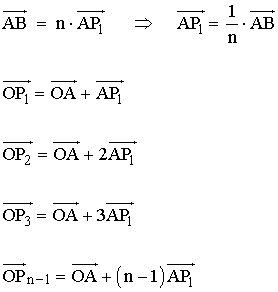


 INICIO
INICIO

