Recuento de resultados y diagrama de árbol
Principio de multiplicación
El método del producto es un método de conteo que consiste en descomponer el experimento n en otros experimentos más simples n1, n2, n3... y multiplicar el número de posibilidades de cada experimento. Por tanto todos los experimentos juntos pueden hacerse de: n1· n2· n3· ... formas diferentes.
Ejemplo 1:
En un restaurante el menú se pueden elegir
entre tres primeros platos, tres segundos y
cuatro postres. ¿Cuántos menús diferentes
se pueden pedir?
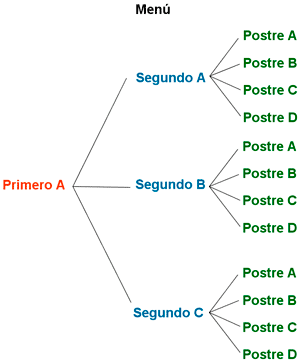
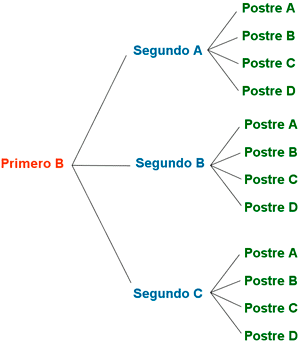
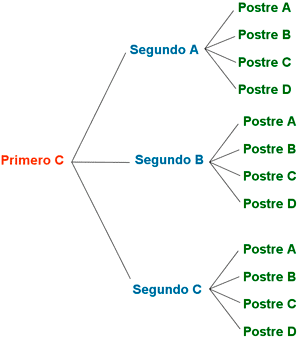
Elaborando el diagrama de árbol se observa que
por cada primer plato podemos elegir tres
segundos y por cada segundo se pueden elegir
cuatro postres distintos. Por tanto
hay 3·3·4 = 36 menús diferentes.
Ejemplo 2:
En una tienda on-line tienen las siguientes
prendas para la temporada de verano: 4
tipos distintos de camiseta, 3 tipos de
pantalones y 2 tipos de calzado. ¿Cuántos
grupos de prendas podemos elegir para vestir?
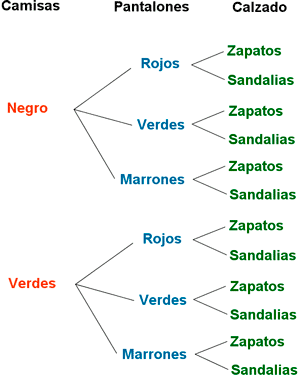
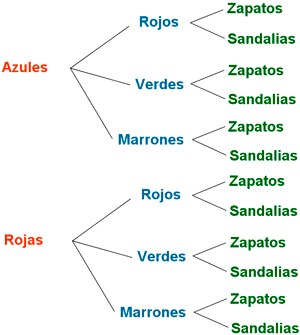
Elaborando el diagrama de árbol se observa que
por cada tipo de camisa podemos elegir tres
pantalones distintos y por cada pantalon podemos
elegir dos tipos de calzado. Por tanto hay
4·3·2 = 24 conjuntos de ropa diferentes.
Ejemplo 3:
Lanzamos simultáneamente una moneda y un dado de seis caras numeradas del 1 al 6.
Describe cuántas y cuáles son las posibilidades del experimento. Haz un diagrama de árbol.
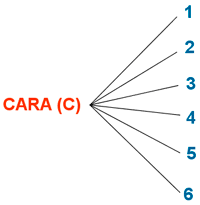
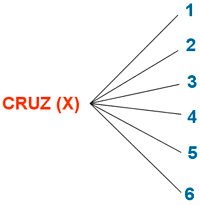
El número de posibilidades del experimento es 12: C1 C2 C3 C4 C5 C6 X1 X2 X3 X4 X5 X6
Nº de posibilidades aplicando el método del producto es 2·6 = 12
Principio de adición
El método de adición es un método de conteo que consiste en descomponer un experimento n en otros experimentos excluyentes más simples n1, n2, n3... y sumar el número de posibilidades de cada experimento. Por tanto todos los experimentos juntos pueden hacerse de: n1+ n2+ n3+ ... formas diferentes.
Ejemplo 4:
Lanzamos al aire dos monedas: una de 2€ , una de 1€ y una de 0.20€. ¿De cuántas
formas diferentes se pueden obtener una o dos caras?
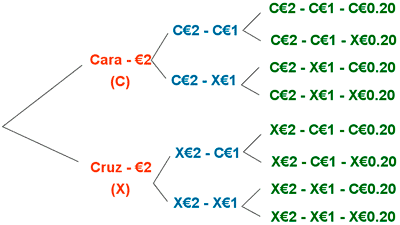
Obtenemos una cara en : A = { C€2-X€1-X€0.20 X€2-C€1-X€0.20 X€2-X€1-C€0.20 }
Obtenemos dos caras en : B = { C€2-C€1-X€0.20 C€2-X€1-X€0.20 X€2-C€1-C€0.20 }
Obtenemos tres caras en : C = { C€2-C€1-C€0.20 }
Ningún resultado pertenece a conjuntos distintos.
Utilizamos el principio de adición: tenemos que para obtener una, dos o tres caras, son : 3 + 3 + 1 = 7 modos
En el diagrama de árbol también vemos que hay 7 formas de obtener una, dos o tres caras.


 INICIO
INICIO
