Problemas resueltos de distribución normal II.
1) La duración media de un lavavajillas es de 15 años, y su desviación típica 0,5. Sabiendo que la vida útil del lavavajillas se distribuye normalmente, hallar la probabilidad de que al adquirir un lavavajillas dure más de 15 años.
2) Las alturas medias en centímetros de cierta población se distribuyen según una normal de media 176 y desviación típica 12. ¿Cuál es la probabilidad de que un individuo elegido al azar mida entre 170 y 190 centímetros?
3) La altura de los candidatos de un llamamiento al Servicio Militar sigue una distribución normal de media 1,7 y desviación típica 0,1. Se desea saber :
a) Probabilidad de que un candidato, elegido al azar, tenga una altura entre 1,7 y 1,9.
b) Si el llamamiento consta de 50.000 candidatos y se excluyen por falta de talla aquellos cuya altura es inferior a 1,5, ¿cuál es el número esperado de exclusiones por esta causa?
4) Una máquina produce recipientes cuyas capacidades están fijadas según una distribución normal N ( 10 ; 0,1 ). Un fabricante considera que un recipiente es defectuoso si su capacidad no está entre 9,9 y 10,1. ¿Qué probabilidad tiene un recipiente de ser considerado defectuoso?
5) La cantidad de café depositada en cada bolsa por una máquina envasadora sigue una distribución normal con media 1040 g y desviación típica de 50 g.
a) Calcula el tanto por ciento de paquetes que contienen más de un kilogramo.
b) Calcula el valor de x sabiendo que el 95,7 % de los paquetes contiene menos de x gramos.
c) Calcula el tanto por ciento de paquetes cuyo contenido tiene un peso comprendido entre 950 y 1050 gramos.
6) En una población, los ingresos anuales siguen una distribución normal, con una media de 20000 € y una desviación típica de 8000 €. Si la proporción de pobres es del 4 % y la de ricos del 2 %, ¿cuáles son los ingresos anuales que marcan los límites de pobreza y riqueza de esa población?
7) En una granja avícola pueden usar dos sitemas de alimentación para sus gallinas : A y B. Con ambos se recoge aproximadamente el mismo número de huevos, pero cuando se usa el sistema A, el peso de los huevos sigue una distribución normal de 62 gramos de media y 3,5 gramos dedesviación típica, mientras que usando el sistema B la distribución, también normal, tiene 63,5 gramos de media y 4,5 gramos de desviación típica. Si hay que desechar, por inutilizables, los huevos de menos de 55 gramos :
a) ¿Qué sistema resulta preferible?
b) ¿Cuántos huevos se desecharon en una temporada en la que se usó el sistema A y se produjeron 1000 docenas de huevos?
8) Los salarios mensuales de los trabajadores del país A sigue una normal N ( 2000, σ ).
a) Calcula σ para que la probabilidad de ganar más de 2100 € sea de 0,33.
b) Sabiendo que los salarios del país B siguen una normal N ( 2000, 200 ), ¿en cuál de los dos países es más fácil ganar más de 2100 € al mes?
9) Cierto tipo de batería dura un promedio de 3 años, con una desviación típica de 0,5 años. Suponiendo que la duración de las baterías es una variable normal :
a) ¿Qué porcentaje de baterías se espera que duren entre 2 y 4 años?
b) Si una batería lleva funcionando 3 años, ¿cuál es la probabilidad de que dure menos de 4,5 años?
10) El contenido de las botellas de una bodega de vino albariño sigue una ditribución normal de media 75 cl y desviación típica 2 cl. Calcula :
a) El porcentaje de botellas cuyo contenido esté entre 71 y 79 cl.
b) La probabilidad de que una botella tenga un contenido superior a los 73 cl si se sabe que es inferior a 75 cl.
11) El tiempo necesario para terminar determinado examen sigue una distribución normal con media 60 minutos y desviación típica de 10 minutos. Se pide :
a) ¿Cuánto debe durar el examen para que el 95 % de las personas lo terminen?
b) ¿Qué porcentaje de personas lo terminará antes de 75 minutos?
12) En cierta población humana, la media muestral de una característica se distribuye mediante una distribución muestral. La probabilidad de que dicha media sea menor o igual que 75 es 0,58 y la de que sea mayor que 80 es 0,04.
Hallar la media y la desviación típica de dicha distribución.
( Tamaño muestral n = 100 ).
Problemas resueltos de distribución normal I.
1) Las alturas medias en centímetros de cierta población se distribuyen según una normal de media 176 y desviación típica 12. ¿Cuál es la probabilidad de que un individuo elegido al azar mida entre 170 y 190 centímetros?

2) La altura de los candidatos de un llamamiento al Servicio Militar sigue una distribución normal de media 1,7 y desviación típica 0,1. Se desea saber :
a) Probabilidad de que un candidato, elegido al azar, tenga una altura entre 1,7 y 1,9.
b) Si el llamamiento consta de 50.000 candidatos y se excluyen por falta de talla aquellos cuya altura es inferior a 1,5, ¿cuál es el número esperado de exclusiones por esta causa?

3) Una máquina produce recipientes cuyas capacidades están fijadas según una distribución normal N ( 10 ; 0,1 ). Un fabricante considera que un recipiente es defectuoso si su capacidad no está entre 9,9 y 10,1. ¿Qué probabilidad tiene un recipiente de ser considerado defectuoso?

4) La cantidad de café depositada en cada bolsa por una máquina envasadora sigue una distribución normal con media 1040 g y desviación típica de 50 g.
a) Calcula el tanto por ciento de paquetes que contienen más de un kilogramo.
b) Calcula el valor de a sabiendo que el 95,7 % de los paquetes contiene menos de a gramos.
c) Calcula el tanto por ciento de paquetes cuyo contenido tiene un peso comprendido entre 950 y 1050 gramos.
Consideremos X la variable aleatoria que indica el peso del contenido de una bolsa de café. Esta variable sigue una distribución N ( 1,04 ; 0,05 ).
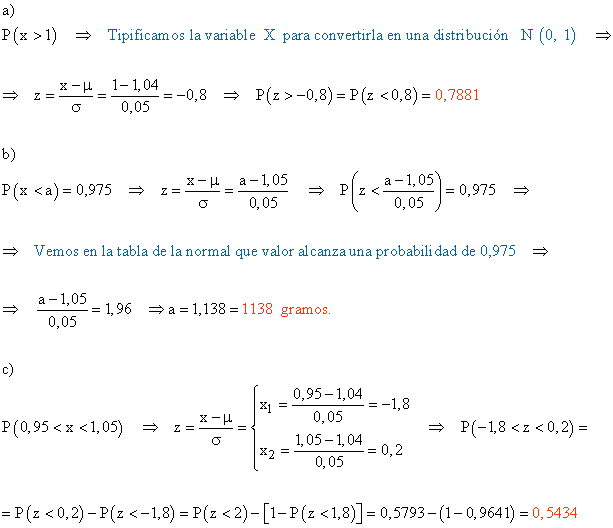
5) En una población, los ingresos anuales siguen una distribución normal, con una media de 20000 € y una desviación típica de 8000 €. Si la proporción de pobres es del 4 % y la de ricos del 2 %, ¿cuáles son los ingresos anuales que marcan los límites de pobreza y riqueza de esa población?
La variable X = "ingresos anuales de una persona" sigue una N ( 20000 ; 8000 ). Se buscan dos valores, a y b tales que P ( x < a ) = 0,04 y P ( x > b ) = 0,02.

6) En una granja avícola pueden usar dos sitemas de alimentación para sus gallinas : A y B. Con ambos se recoge aproximadamente el mismo número de huevos, pero cuando se usa el sistema A, el peso de los huevos sigue una distribución normal de 62 gramos de media y 3,5 gramos dedesviación típica, mientras que usando el sistema B la distribución, también normal, tiene 63,5 gramos de media y 4,5 gramos de desviación típica. Si hay que desechar, por inutilizables, los huevos de menos de 55 gramos :
a) ¿Qué sistema resulta preferible?
b) ¿Cuántos huevos se desecharon en una temporada en la que se usó el sistema A y se produjeron 1000 docenas de huevos?
La variable XA = " peso de un huevo de una gallina alimentada con el sistema A " sigue una distribución normal N ( 62 ; 3,5 ).
La variable XB = " peso de un huevo de una gallina alimentada por el sistema B " sigue una distribución normal N ( 63,5 ; 4,5 ).

7) Los salarios mensuales de los trabajadores del país A sigue una normal N ( 2000, σ ).
a) Calcula σ para que la probabilidad de ganar más de 2100 € sea de 0,33.
b) Sabiendo que los salarios del país B siguen una normal N ( 2000, 200 ), ¿en cuál de los dos países es más fácil ganar más de 2100 € al mes?
La variable XA = " salario de un trabajador del país A " sigue una distribución normal N ( 2000, σ ), y la variable XB = " salario de un trabajador del país B " sigue una N ( 2000, 200 ).
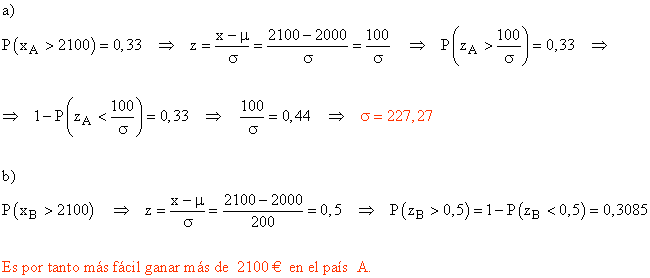
8) Cierto tipo de batería dura un promedio de 3 años, con una desviación típica de 0,5 años. Suponiendo que la duración de las baterías es una variable normal :
a) ¿Qué porcentaje de baterías se espera que duren entre 2 y 4 años?
b) Si una batería lleva funcionando 3 años, ¿cuál es la probabilidad de que dure menos de 4,5 años?
La variable X = " duración en años de una batería " sigue una N ( 3 ; 0,5 ).

9) El contenido de las botellas de una bodega de vino albariño sigue una ditribución normal de media 75 cl y desviación típica 2 cl. Calcula :
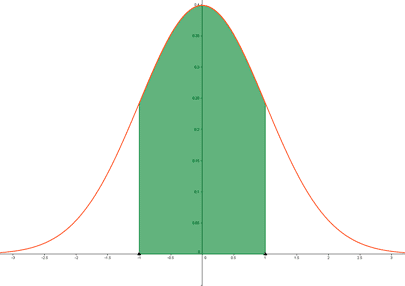
a) El porcentaje de botellas cuyo contenido esté entre 71 y 79 cl.
b) La probabilidad de que una botella tenga un contenido superior a los 73 cl si se sabe que es inferior a 75 cl.
La variable X = " contenido en cl de una botella de vino " sigue una distribución normal N ( 75 , 2 ).
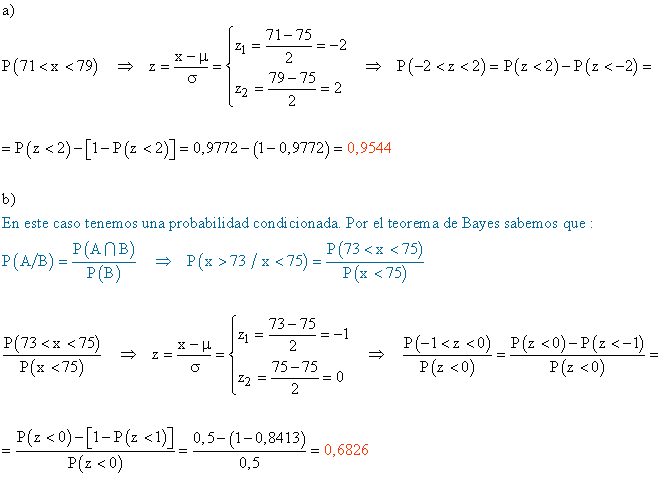
10) La duración media de un lavavajillas es de 15 años, y su desviación típica 0,5. Sabiendo que la vida útil del lavavajillas se distribuye normalmente, hallar la probabilidad de que al adquirir un lavavajillas dure más de 15 años.
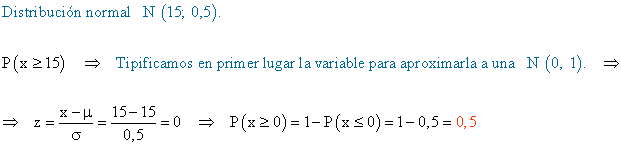
11) El tiempo necesario para terminar determinado examen sigue una distribución normal con media 60 minutos y desviación típica de 10 minutos. Se pide :
a) ¿Cuánto debe durar el examen para que el 95 % de las personas lo terminen?
b) ¿Qué porcentaje de personas lo terminará antes de 75 minutos?
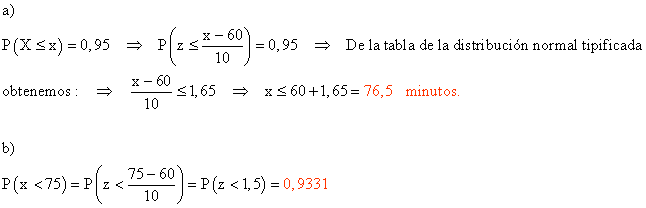
12) En cierta población humana, la media muestral de una característica se distribuye mediante una distribución muestral. La probabilidad de que dicha media sea menor o igual que 75 es 0,58 y la de que sea mayor que 80 es 0,04.
Hallar la media y la desviación típica de dicha distribución.
( Tamaño muestral n = 100 ).



 INICIO
INICIO