Problemas resueltos de integrales definidas y áreas por definición
1) Calcula las suma superiores e inferiores de la función f ( x ) = x2 + 1 en el intervalo [ -3, 3 ] tomando una partición en este intervalo. Realiza la gráfica.
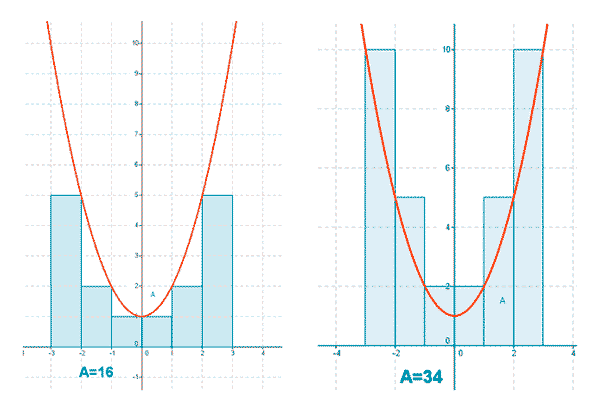
Tomamos la partición P = { -3, -2, -1, 0, 1, 2, 3 }
Para esta partición las sumas superior e inferior son:
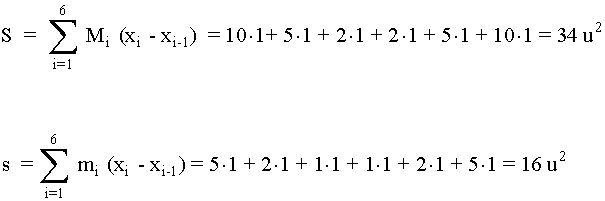
2) Calcula las suma superiores e inferiores de la función f ( x ) = √x en el intervalo [ 3, 9 ] tomando una partición en este intervalo. Realiza la gráfica.
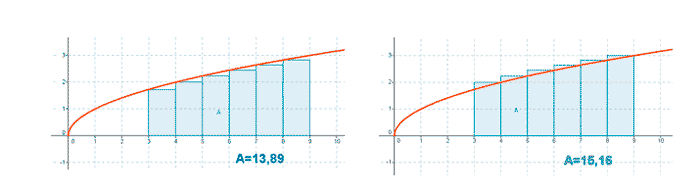
Tomamos la partición P = { 3, 4, 5, 6, 7, 8, 9 }
Para esta partición las sumas superior e inferior son:
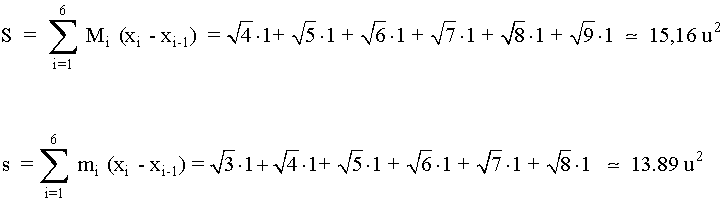
3) Calcula las suma superiores e inferiores de la función f ( x ) = 1/x en el intervalo [ 1, 3 ] para dos particiones distintas de este intervalo, una más fina que la otra. Realiza la gráfica.
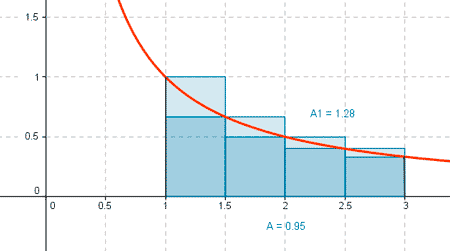
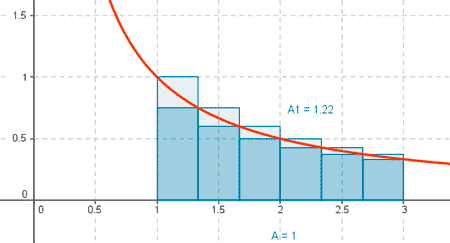
Tomamos las particiones
P = { 1, 1.5, 2, 2.5, 3 }
Para esta partición las sumas superior e inferior son:
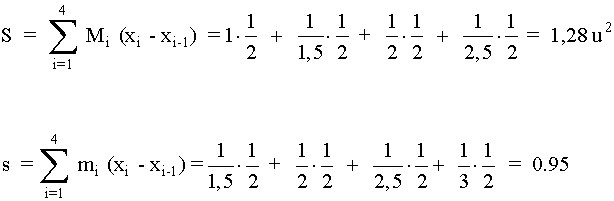
P' ={ 1, 1 + 1/3, 1 + 2/3, 2, 2 + 1/3, 2 + 2/3, 3}
Para esta partición las sumas superior e inferior son:
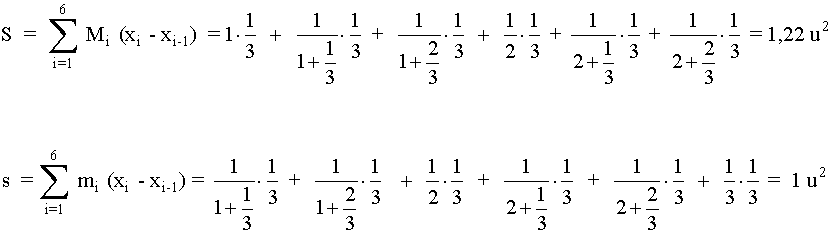
4) Hallar, aplicando la definción de integral, el área de la región delimitada por la recta f ( x ) = x y el eje de abscisas entre las rectas x = 0 y x = 1.
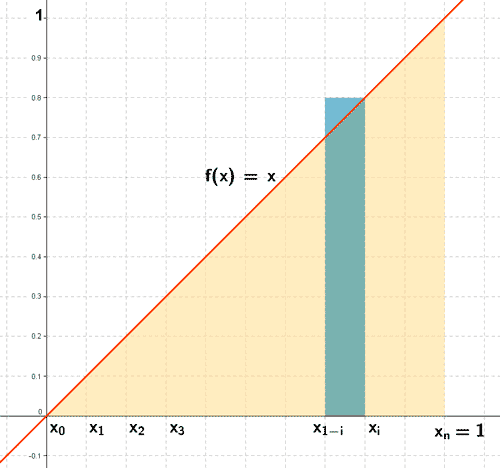
Vamos a tomar la partición del intervalo [0,1] que lo divide en n partes iguales. Sea
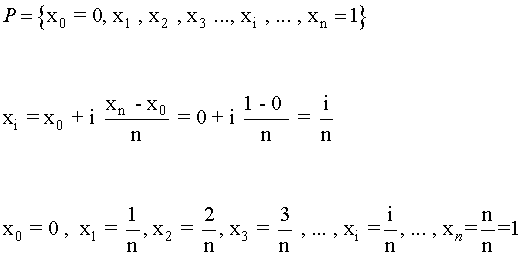
Cada intervalo de la partición tendrá una amplitud de 1/n:
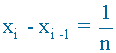
Como la función f(x)=x es creciente, tenemos que, en cada intervalo [ xi-1 , xi ] de la partición se verifica que:
![]()
Teniendo en cuenta todo esto,
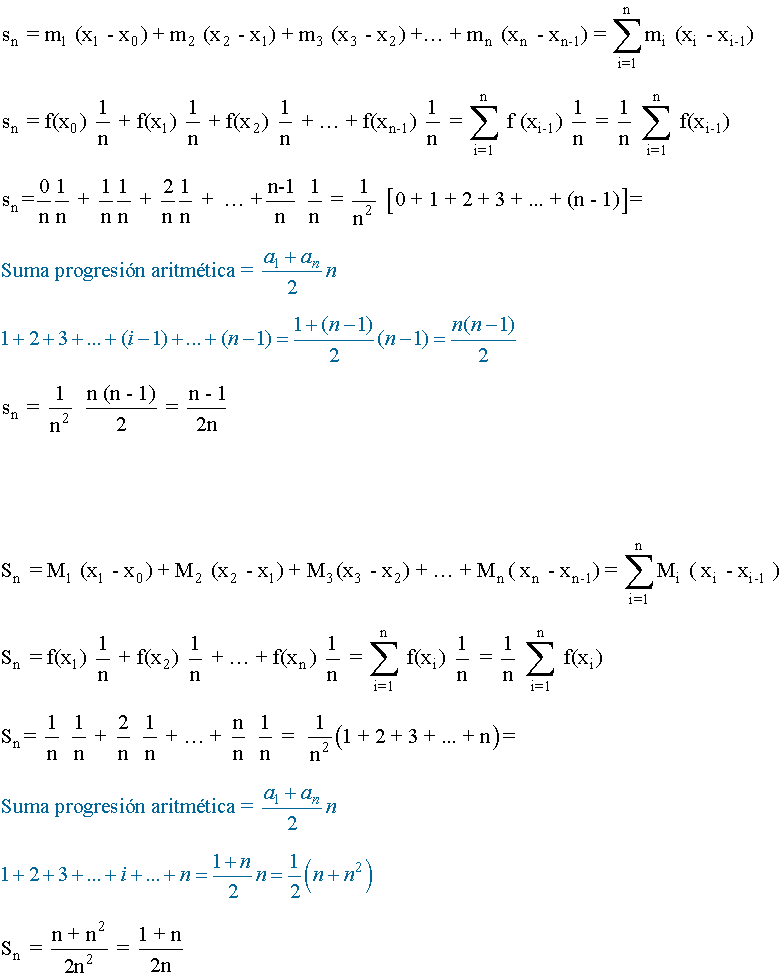
De manera que, los límites de las sumas superiores e inferiores son:

Ambos límites son iguales:
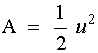
Como f(x) = x es una función integrable en [ 0, 1 ], podemos afirmar que:
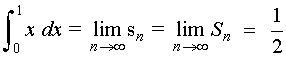
5) Hallar, aplicando la definción de integral, el área de la región delimitada por la recta f ( x ) = x2 y el eje de abscisas entre las rectas x = 0 y x = 2.
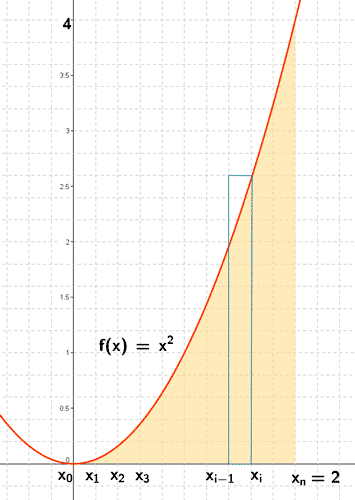
Vamos a tomar la partición del intervalo [0,2] que lo divide en n partes iguales. Sea
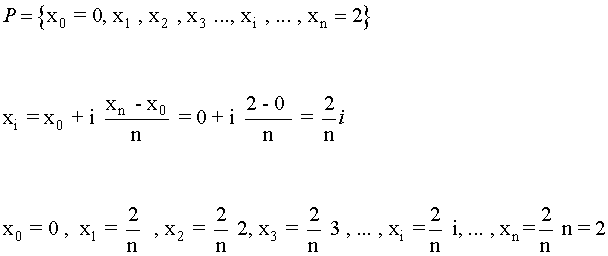
Cada intervalo de la partición tendrá una amplitud de 2/n:
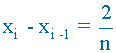
Como la función f ( x ) = x2 es creciente, tenemos que, en cada intervalo [ xi-1 , xi ] de la partición se verifica que:

Teniendo en cuenta todo esto,
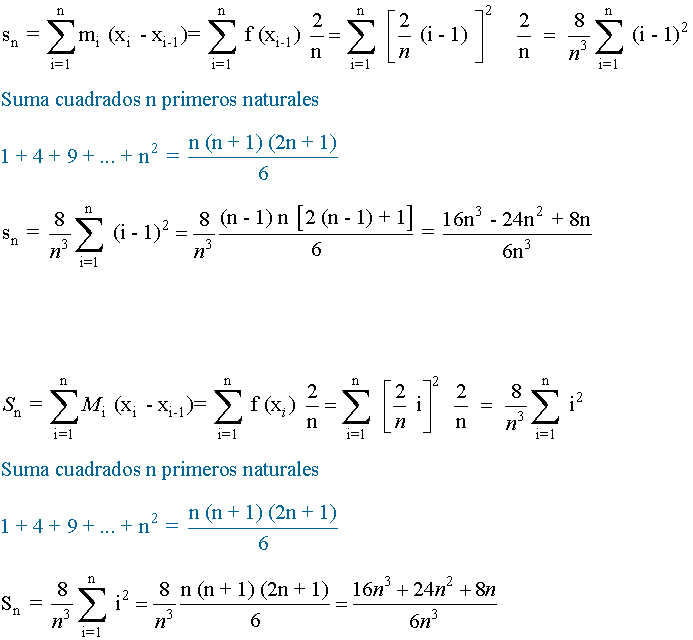
De manera que, los límites de las sumas superiores e inferiores son:

Ambos límites son iguales:
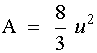
Como f(x) = x2 es una función integrable en [ 0, 2 ], podemos afirmar que:
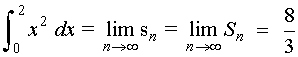
6) Hallar, aplicando la definción de integral, el área de la región delimitada por la recta f ( x ) = x3 y el eje de abscisas entre las rectas x = 0 y x = 1.
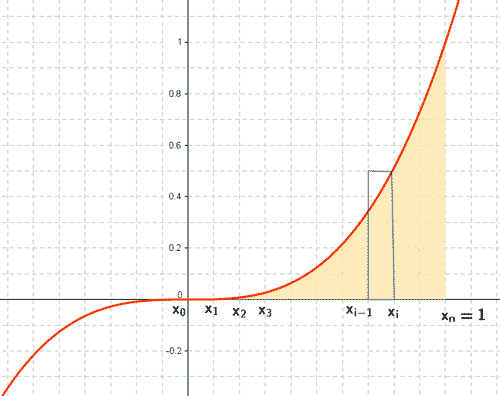
Vamos a tomar la partición del intervalo [0,2] que lo divide en n partes iguales. Sea
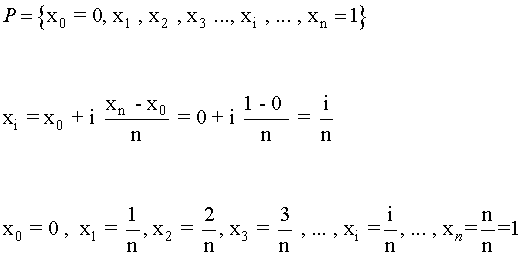
Cada intervalo de la partición tendrá una amplitud de 1/n:
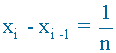
Como la función f ( x ) = x3 es creciente, tenemos que, en cada intervalo [ xi-1 , xi ] de la partición se verifica que:

Teniendo en cuenta todo esto,
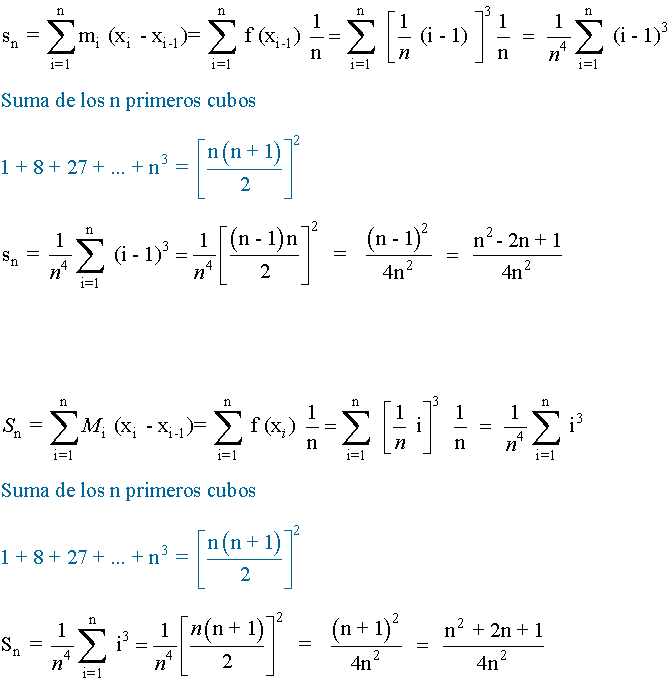
De manera que, los límites de las sumas superiores e inferiores son:

Ambos límites son iguales:
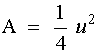
Como f(x) = x3 es una función integrable en [ 0, 1 ], podemos afirmar que:
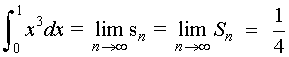
7) Hallar, aplicando la definción de integral, el área de la región delimitada por la recta f ( x ) = ex y el eje de abscisas entre las rectas x = 0 y x = 2.
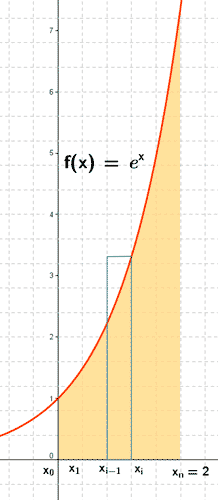
Vamos a tomar la partición del intervalo [0,2] que lo divide en n partes iguales. Sea
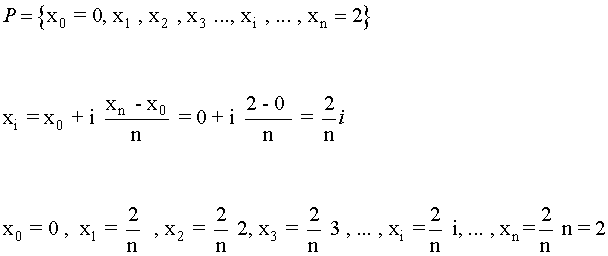
Cada intervalo de la partición tendrá una amplitud de 2/n:
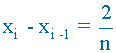
Como la función f ( x ) = ex es creciente, tenemos que, en cada intervalo [ xi-1 , xi ] de la partición se verifica que:
![]()
Teniendo en cuenta todo esto,
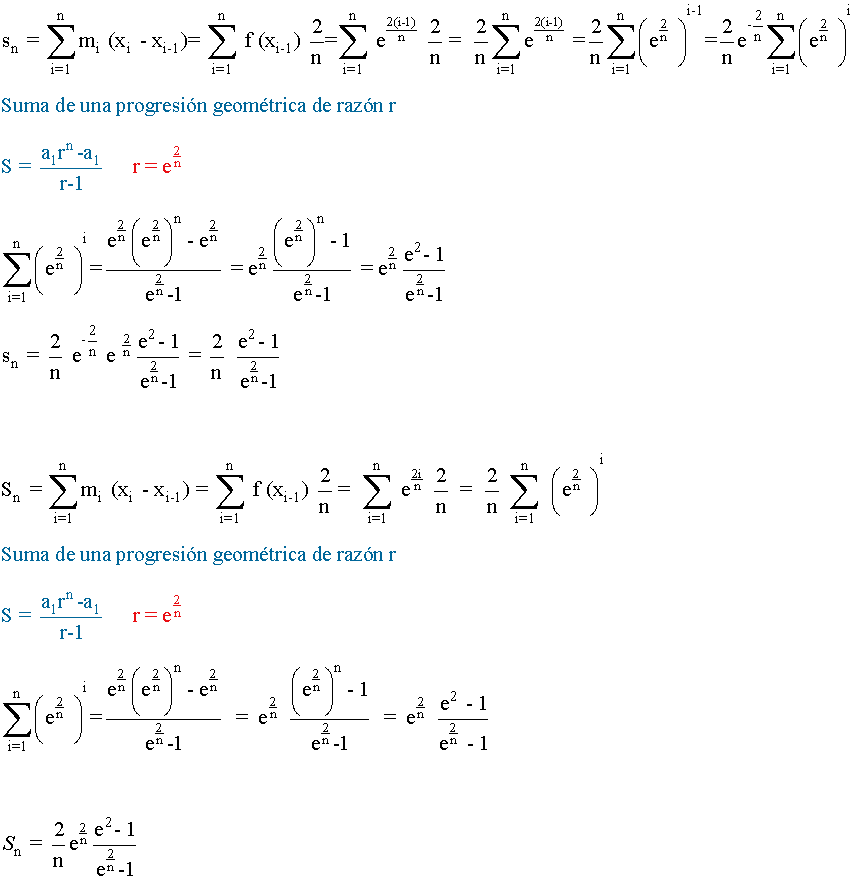
De manera que, los límites de las sumas superiores e inferiores son:
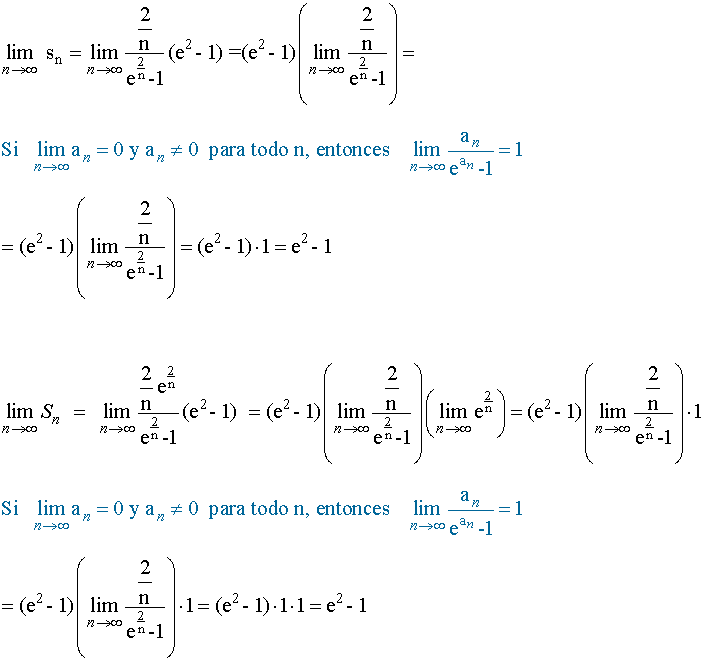
Ambos límites son iguales:
![]()
Como f(x) = ex es una función integrable en [ 0, 2 ], podemos afirmar que:
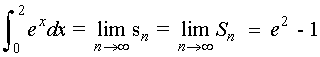
8
9


 INICIO
INICIO