Problemas resueltos de optimización I
Figuras planas
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Cuadrado |  |
P = 4a | A = a2 |
| Rectángulo |  |
P = 2b + 2a | A = ba |
| Rombo | 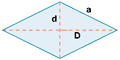 |
P = 4a | |
| Romboide | 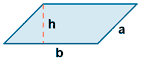 |
P = 2a + 2b | A = b h |
| Trapecio | 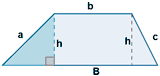 |
P = a + B + b + c | |
| Trapecio isósceles |
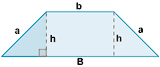 |
P = 2a + B + b | |
| Triángulo | 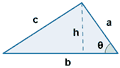 |
P = a + b + c |
|
| Triángulo equilátero |
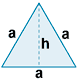 |
P = 3a |
|
| Triángulo rectángulo |
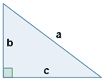 |
P = a + b + c a2 = b2 + c2 |
|
| Hexágono regular |
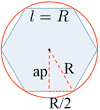 |
P = 6l = 6R ap = apotema |
|
| Pentágono regular |
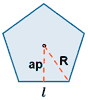 |
P = 5l | ap = apotema |
| Círculo | 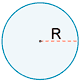 |
L = 2πR | A = πR2 |
| Sector circular |
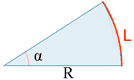 |
L = R α P = 2R + L |
|
| Corona circular |
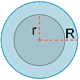 |
L = 2π (R + r) | A = π (R2 - r2) |
| Elipse | 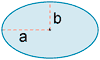 |
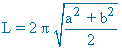 |
A = π a b |
Cuerpos en el espacio
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Cubo | 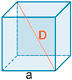 |
A = 6 a2 |
V = a3 |
| Ortoedro | 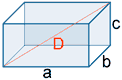 |
A = 2( a·b + a·c + b·c ) |
V = a · b · c |
| Prisma | 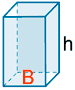 |
PB = perímetro de la base AL = PB · h AT = AL + 2·AB |
V = AB h |
| Pirámide | 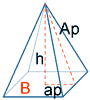 |
PB = perímetro base Ap = apotema pirámide ap = apotema de la base Ap2 = h2 + ap2 AT = AL + AB |
|
| Cilindro | 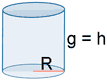 |
AL = 2 π R h AB =2 π R2 AT = 2 π R (h + R) |
V = π R2 h |
| Cono | 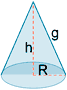 |
g2 = R2 + h2 AL = π R g AB = π R2 AT = π R (g + R) |
|
| Tronco de cono |
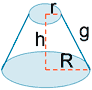 |
AL = π (R + r) g AT = π [ g(R + r) + R2 + r2 ] |
|
| Esfera | 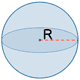 |
A = 4 π R2 | |
| Cuña | 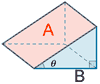 |
A = área cara superior AB = área base A = AB sec θ |
Descomponer el número 80 en dos sumandos cuyo producto sea máximo.
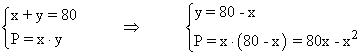
Para hallar el máximo de la función, calculamos su derivada e igualamos a 0:
P ' (x) = 80 - 2x = 0 ⇔ 2x = 80 ⇔ x = 40
Además, tenemos que: P '' (x) = -2 < 0 ⇒ Máximo
Por lo tanto, los números son: x = 40 y = 40
SELECTIVIDAD
Un número más el cuadrado de otro número suman 48. ¿Cómo deben elegirse dichos números para que su producto sea máximo?
Las condiciones del problema son las siguientes:
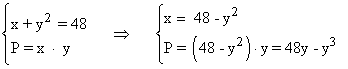
Por lo tanto tenemos que optimizar la siguiente función: P(y) = 48y - y3
Calculamos la primera derivada e igualamos a 0:
P ' (y) = 48 - 3y2 = 0 ⇔3y2 = 48 ⇔ y2 = 16 ⇔ y = 4 (descartamos la solución negativa)
Comprobamos que la solución es un máximo mediante la segunda derivada:
P '' (y) = -6y ⇒ P ''(4) = -24 < 0 ⇒ Máximo
Por tanto los dos números que buscamos son:
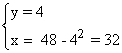
SELECTIVIDAD
Un agente comercial cobra por la venta de mercaderías una comisión:
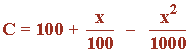
donde x representa la cantidad en miles de pesetas de la venta efectuada. Determinar la cantidad que habrá que vender para que la comisión que haya que pagar sea máxima.
Para encontrar el máximo tenemos que calcular la derivada de la función e igualarla a 0:
![]()
![]()
Vamos a comprobar si x = 5 es máximo de la función:
![]()
En particular, C'' < 0 para x = 5 , luego es máximo de la función.
Para x = 5 la comisión será máxima, y valdrá:
![]()
Una persona quiere vallar un campo rectangular de 10.000 m2 de superficie. ¿Cuáles serán las dimensiones para que el coste sea mínimo?
1) Para resolver un problema de optimización debemos encontrar una función a la que calcularle sus extremos (máximos o mínimos).
Por lo tanto tenemos que localizar las variables que definan la función que queremos optimizar.
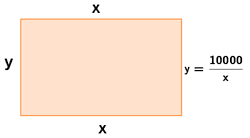
En nuestro caso las variables que definen a la superficie corresponden al ancho (x) y alto (y) del campo:
S = x · y ⇒ 10.000 = x · y
A continuación despejamos una de ellas en función de la otra:
![]()
La función que queremos minimizar es la función perímetro dada por:
P = 2x + 2y
Sustituimos en P el valor de y , de manera que nos queda P en función de x :
![]()
2) Calculamos la primera derivada de P y la igualamos a 0:
![]()
Resolvemos la ecuación:
![]()
Para x = - 100 no tiene sentido el problema ya que la longitud tiene que ser positiva.
Comprobamos que para x = 100 la función tiene un mínimo:
![]()
![]()
3) Calculamos las imágenes de los extremos:
![]()
SELECTIVIDAD
Se dispone de 3.000 € para vallar un terreno rectangular colindante con un camino recto. Si el precio de la valla que ha de ponerse en el lado del camino es de 10 €/metro y el de la valla de los restantes lados es de 2 €/metro , ¿cuáles son las dimensiones y el área del terreno rectangular de área máxima que se puede vallar?
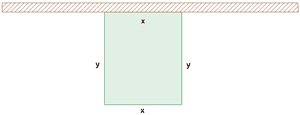
Puesto que la forma del terreno es rectangular, llamaremos x a su base e y a su altura.
Supongamos que es el lado x el que está situado junto al camino.
Entonces, el precio total del vallado será la suma del coste de cada lado:
3.000 = 10x + 2y + 2y + 2x ⇒ 3.000 = 12x + 4y ⇒ y = 750 - 3x
Reuniendo dicha expresión junto con la fórmula del área del rectángulo tenemos:
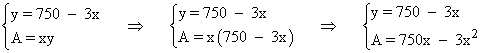
Para encontrar un máximo de la función área tenemos que calcular su derivada e igualarla a 0:
A '(x) = 750 - 6x = 0 ⇒ 6x = 750 ⇒ x = 125 metros
Comprobamos que es un máximo estudiando el signo de la segunda derivada:
A ''(x) = - 6 < 0 para cualquier valor de x
Por tanto, x = 125 m. maximiza el área del rectángulo.
y = 750 - 3x = 750 - 3·125 = 375 metros
Las dimensiones del rectángulo deberán ser 125 m. y 375 m. .
SELECTIVIDAD
Sea T un triángulo de perímetro 60 centímetros. Uno de los lados del triángulo T mide x cm y los otros lados tienen la misma longitud.
a) Deducir razonadamente las expresiones de las funciones A y f tales que:
A(x) = Área del triángulo T
f(x) = [A(x)]2
Indicar además entre qué valores puede variar x .
b) Obtener, razonadamente, el valor de x para el que f(x) obtiene el valor máximo.
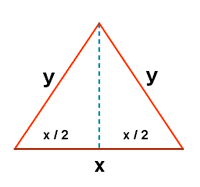
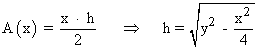
Como sabemos que: x + 2y = 60
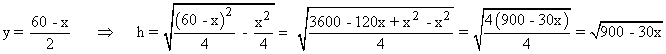
Por lo tanto tenemos que:
![]()
Una vez calculada la función A(x) tenemos que:
![]()
Para obtener el valor máximo de la función, calculamos la primera derivada e igualamos a 0:
![]()
![]()
![]()
Para comprobar que x = 20 es un máximo calculamos la segunda derivada:
![]()
![]()
Por lo tanto, en x = 20 la función alcanza su máximo.
SELECTIVIDAD
Determinar el mayor área que puede encerrar un triángulo rectángulo cuyo lado mayor mida 1 metro.
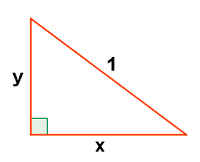
En un triángulo rectángulo, el mayor lado corresponde con la hipotenusa:
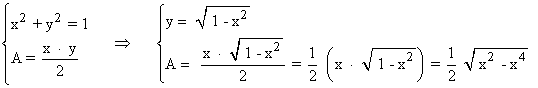
Para determinar el mayor área, calculamos la primera derivada y la igualamos a 0:
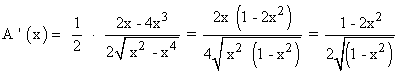
![]()
Descartamos la raíz negativa de la anterior ecuación puesto que a > 0 .
Para comprobar que dicho valor es un máximo, calculamos la segunda derivada:
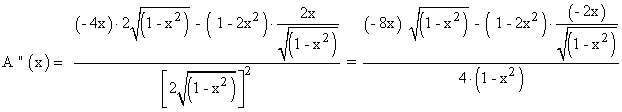
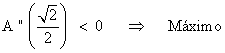
Por lo tanto, las dimensiones serían las siguientes:
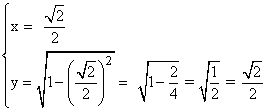
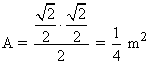
SELECTIVIDAD
Calcula el área máxima que puede tener un triángulo rectángulo tal que la suma de las longitudes de sus dos catetos vale 4 cm.
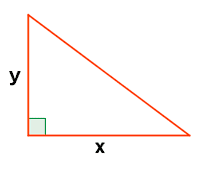
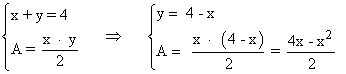
Para hallar el valor máximo, calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que corresponde con un máximo:
![]()
Por lo tanto, la solución es la siguiente:
![]()
SELECTIVIDAD
Un solar rectangular de 11.250 m2 se divide en tres zonas rectangulares iguales para venderlo. Se valla el borde del campo y la separación de las zonas. Calcula las dimensiones del solar para que la longitud de valla utilizada sea mínima.
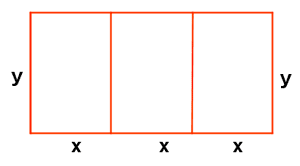
A partir de la superficie del solar, despejamos la variable y y sustituimos en la función que define la longitud de la valla a utilizar:
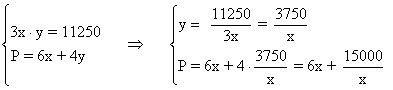
Para hallar el valor mínimo, calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que se trata de un mínimo a través de la segunda derivada:
![]()
Por lo tanto la solución es la siguiente:
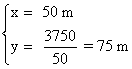
SELECTIVIDAD
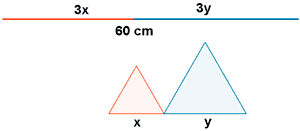
Con 60 centímetros de alambre se construyen dos triángulos equiláteros cuyos lados miden x e y . ¿Qué valores de x e y hacen que la suma de las áreas de los triángulos sea mínima?
Recordamos que la altura y el área de un triángulo equilátero viene dada por:
![]()
![]()
donde a es el lado del triángulo equilatero.
Los 60 cm deben ser igual a la suma de los perímetros de ambos triángulos.
60 = 3x + 3y ⇒ 20 = x + y
Planteamos la condición anterior junto con la función suma de las áreas:
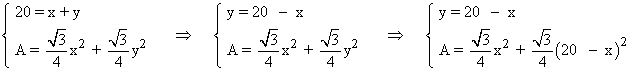
Simplificamos la función área:
![]()
Para encontrar un mínimo de la función área calculamos su derivada e igualamos a 0 :
![]()
Comprobamos que es un mínimo calculando la segunda derivada:
A ''(x) = √3 > 0 para cualquier valor de x
Luego x = 10 cm es un mínimo de la función.
Si x = 10 ⇒ y = 20 - x = 20 - 10 = 10 cm
Las dimensiones pedidas son x = 10 cm , y = 10 cm .
SELECTIVIDAD
Se dispone de un hilo metálico de longitud 140 m. Se quiere dividir dicho hilo en tres trozos de forma que uno de ellos tenga longitud doble de otro y tal que al construir con cada uno de ellos un cuadrado, la suma de las áreas de los tres cuadrados sea mínima. Encontrar la longitud de cada trozo.
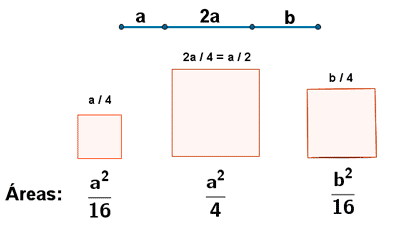
Las condiciones que nos da el problema son las siguientes:
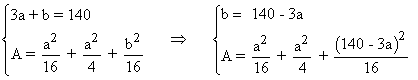
![]()
Para hallar el valor mínimo, calculamos la primera derivada e igualamos a 0:
![]()
![]()
Comprobamos que se trata de un mínimo mediante la segunda derivada:
![]()
Por lo tanto el hilo se tiene que dividir en tres trozos de 30 m , 60 m y 50 m.
SELECTIVIDAD
Un alambre de longitud 1 metro se divide en dos trozos, con uno se forma un cuadrado y con el otro una circunferencia. Calcula las longitudes de los dos trozos para que la suma de las áreas de ambos recintos sea mínima.
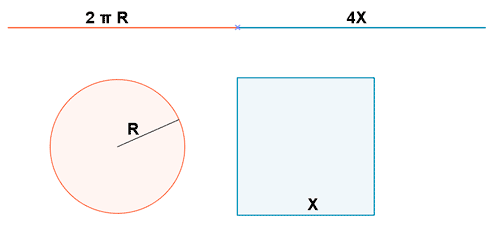
![]()
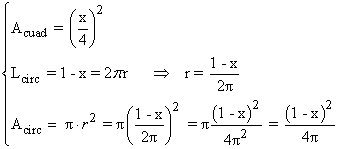
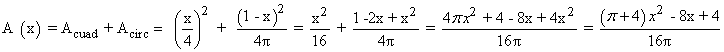
Para hallar el valor que hace mínima a la función, calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que se trata de un mínimo mediante la segunda derivada:
![]()
Por lo tanto, el valor mínimo de la suma de las áreas se obtiene cuando:
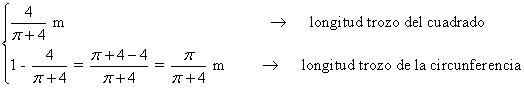
SELECTIVIDAD
Un jardinero desea construir un parterre con forma de sector circular. Si dispone de 20 metros de alambre para rodearlo, ¿qué radio debe tener el sector para que el parterre tenga la mayor superficie posible? ¿cuál será la amplitud en radianes del sector?
Un sector circular es una porción de un círculo tal y como se muestra en la figura.
Las condiciones que nos da el problema son las siguientes:

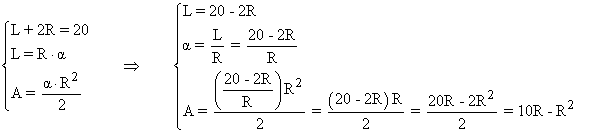
Para optimizar la función obtenida, calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que se trata de un valor máximo calculando la segunda derivada:
![]()
Por lo tanto, para que el área del sector circular sea máxima el radio tiene que ser de 5 metros.
Por otra parte, la amplitud en radianes puede calcularse a través de las siguientes fórmulas:
![]()
De entre todos los sectores circulares de área 1, hallar el de perímetro mínimo.
Las condiciones que nos determina el problema son las siguientes:
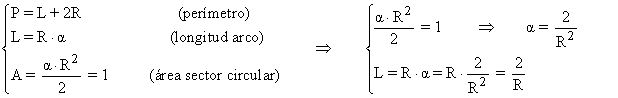
Por lo tanto, la función a optimizar es:
![]()
A continuación calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que R = 1 es un mínimo (descartamos la solución negativa al no tener sentido geométrico):
![]()
Por lo tanto, el sector circular de área 1 cuyo perímetro es mínimo es el de radio 1.



 INICIO
INICIO