Problemas que se resuelven con inecuaciones

Hallar los números naturales cuyo triple menos seis unidades es mayor que su duplo más cinco unidades.

Sea  x  uno cualquiera de los números pedidos.

El triple de x menos 6 es:     3x - 6

El duplo de x más 5 unidades es:     2x + 5

3x - 6 > 2x + 5

Resolvemos la inecuación:

            3x - 6 > 2x + 5     ⇔     3x - 2x > 5 + 6     ⇔     x > 11

Los números naturales mayores que 11 son los que cumplen las condiciones del problema.

¿Qué números reales verifican que su cuadrado es menor que su cuádruplo?

Sea  x  uno cualquiera de los números pedidos.

Si el cuadrado de x es menor que su cuádruplo tenemos:

x² < 4x

Resolvemos la inecuación:

            x² < 4x     ⇔     x² - 4x < 0     ⇔     x(x - 4) < 0

            x(x - 4) = 0      ⇔     x = 0    ó    x - 4 = 0

            x = 0

            x - 4 = 0     ⇔     x = 4

Estudiamos el signo en los intervalos:    (-∞ 0) , (0 , 4) , (4 , ∞)

•  (-∞ , 0):    x = - 1     ⇒     x(x - 4) = (-1)(-1 - 4) > 0

•  (0, 4):    x = 1     ⇒     x(x - 4) = 1(1 - 4) < 0

•  (4 , ∞):    x = 5     ⇒     x(x - 4) = 5(5 - 4) > 0

(- ∞, 0)	(0 , 4)	(4 , ∞)
+	-	+

El conjunto de soluciones es:    (0 , 4)

María tiene 10 años menos que Pedro. ¿Cuántos años puede tener María, si sabemos que el triple de su edad es mayor que el doble de la de Pedro?

Sea  x  la edad de María.

Entonces, la edad de Pedro es:    x + 10

Según el problema, el triple de  x  es mayor que el doble de  (x + 10), luego:

3x > 2(x + 10)

Resolvemos la inecuación:

            3x > 2x + 20     ⇔     x > 20

Por tanto, María tendrá más de 20 años.

Halla las dimensiones de los cuadrados de área menor que 36 m².

Sea  x  la longitud del lado del cuadrado.

El área de un cuadrado es:     x²

Queremos los cuadrados cuya área sea menor que 36 m², por tanto:

x² < 36

x² < 36     ⇔     x² - 36 < 0

x² - 36 = 0     ⇔     x = ± 6

Podemos factorizar la inecuación:     (x - 6)(x + 6) < 0

Los intervalos a estudiar son:     (-∞ , - 6) , (-6 , 6) , (6 , ∞)

Sin embargo, como la longitud de los lados tiene que ser un número positivo, sólo estudiaremos el signo en los siguientes intervalos:

•  (0 , 6):  x = 1     ⇒     (x - 6)(x + 6) = (1 - 6)(1 + 6) < 0

•  (6 , ∞):  x = 7     ⇒     (x - 6)(x + 6) = (7 - 6)(7 + 6) > 0

(0 , 6)	(6 , ∞)
-	+

El lado de aquellos cuadrados que tengan área menor que 36 m² estará contenido en el intervalo:     (0 ,6)

Por tanto los lados serán menores que  6 m.

Deseamos construir un cuadro de forma cuadrada. El interior del cuadrado es de madera que vale a 20 euros el metro cuadrado y el marco de bronce cuesta 45 euros el metro. ¿Qué longitud tendrá como máximo el lado del cuadrado si no disponemos de más de 875 euros?

Sea  x  el lado del cuadrado.

El precio del interior del cuadro será en total:     20x²

Y el precio del marco será en total:     4x · 45

El precio total del cuadro no debe superar los 875 euros que tenemos, por tanto:

20x² + 45 · 4x ≤ 875

Resolvemos la inecuación:

            20x² + 4x·45 ≤ 87520     ⇔     x² + 180x - 875 ≤ 0

           x² + 180x - 875 = 0

            

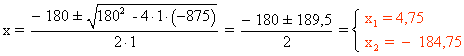
Factorizamos la ecuación de segundo grado:     (x - 4,75)(x + 184,75) = 0

Los intervalos a estudiar serían:     (-∞ , - 184,75) , (-184,75 , 4,75) , (4,75 , ∞)

Sin embargo, como la longitud tiene que ser un número real positivo, sólo estudiaremos el signo en los siguientes intervalos:

•  (0 , 4,75):    x = 1     ⇒     (x - 4,75)(x + 184,75) = (1 - 4,75)(1 + 184,75) < 0

•  (4,75 , ∞):    x = 5     ⇒     (x - 4,75)(x + 184,75) = (5 - 4,75)(5 + 184,75) > 0

(0 , 4,75)	(4,75 , ∞)
-	+

El conjunto de soluciones es:     (0 , 4,75]

Incluimos el valor   x = 4,75  , ya que la inecuación contiene el signo menor o igual.

Por tanto, el lado del cuadro tendrá una longitud máxima de  4,75  metros.