La recta real
Representación de los números enteros
La representación de números enteros se hace de forma sencilla sin más que llevar la distancia entre 0 y 1 tantas veces como sea preciso sobre la recta, hacia la derecha si el número es positivo o hacia la izquierda si es negativo.
![]()
Representación de los números racionales
Los números racionales se representan dividiendo segmentos de la recta en partes iguales con la ayuda del teorema de Tales.
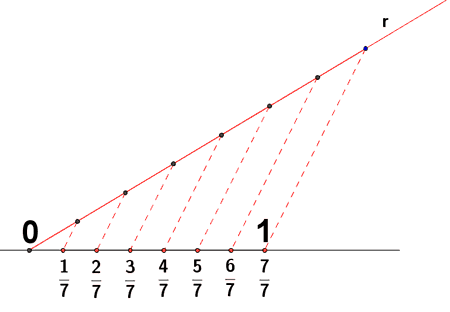
Trazamos una semirrecta r a partir de A. Sobre ella marcamos con el compás 7 segmentos iguales, de la longitud que queramos. Unimos la última marca con B y trazamos paralelas, una por cada marca de la semirrecta.
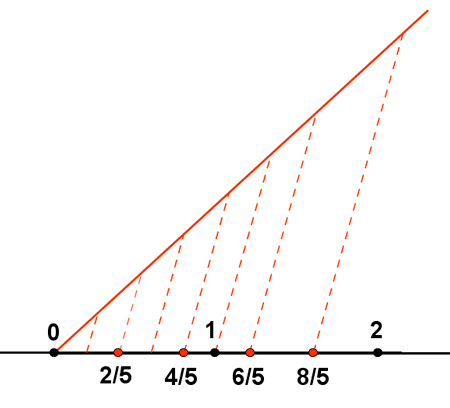
NOTAS DE CLASE: Representación de un número racional
Para representar un número fraccionario se divide la unidad tantas veces como indica el denominador y de estas se toman tantas como indica el numerador. Para 2/5 se divide la unidad en 5 partes iguales y de éstas se toman 2.
NOTAS DE CLASE: Representación de un número decimal
Para representar 0,7 se divide la unidad en 10 partes iguales y se toman 7
Para representar 0,45 se divide la unidad en 100 partes iguales y se toman 45
Para representar 0,753 se divide la unidad en 1000 partes iguales y se toman 753
Representación de los números reales
Los números reales llenan por completo la recta, de ahí que la llamemos recta real.
A cada punto de la recta real le corresponde un número real, y a cada número real le corresponde un punto de la recta.
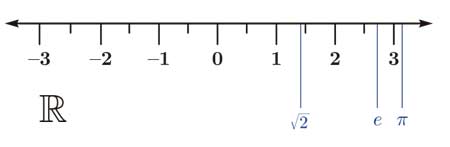
√2=1,41421356... e=2,718281828459... π=3,141592653...
Algunos números, en particular algunos números irracionales, pueden ser representados de manera exacta utilizando el teorema de Pitágoras una o sucesivas veces.
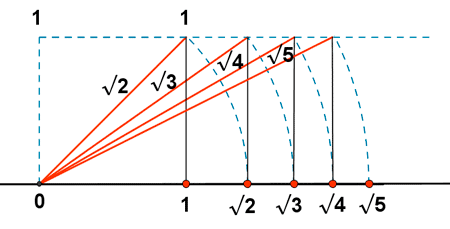
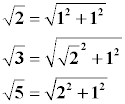
Los restantes números irracionales se representan en la recta real mediante sus aproximaciones decimales.
Ejemplo para representar el número irracional 3,857...
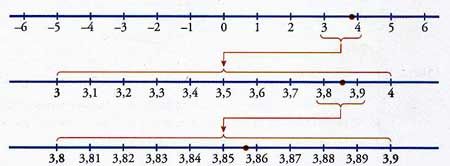


 INICIO
INICIO

