Lenguaje gráfico para interpretar los números complejos.
Interpretación gráfica de igualdades y desigualdades entre complejos.
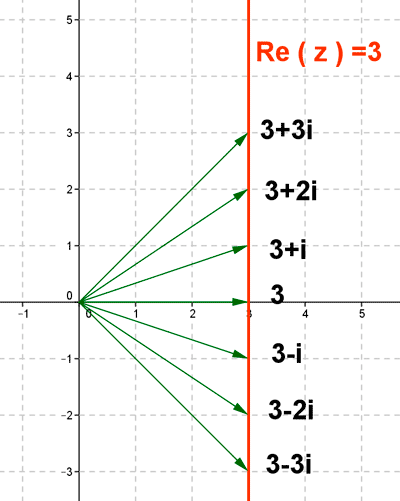
1 ) Representa graficamente donde están situados todos los números complejos cuya parte real vale 3.
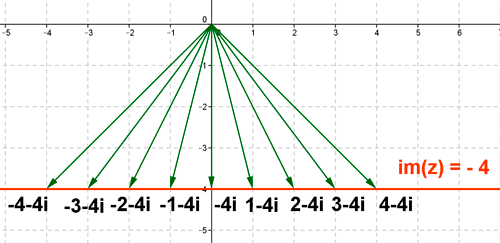
2 ) Representa graficamente donde están situados todos los números complejos cuya parte imaginaria vale - 4.
3 ) Representa graficamente los números complejos que tienen la parte real igual a la parte imaginaria.
4 ) Representa graficamente los números complejos z tales que:
![]()
5 ) Representa graficamente los números complejos que cumple:
![]()
6 ) Representa graficamente los números complejos que cumple:
![]()
7 ) Representa graficamente los números complejos cuyo argumento valga 60º
8 ) Representa los números complejos z tales que:
![]()
9 ) Representa los números complejos z tales que:
![]()
10 ) Representa los números complejos z tales que:
![]()
11 ) Representar graficamente las igualdades siguientes. ¿ Qué figura se determina en cada caso ?
![]()
12 ) Representa los números coplejos z tales que:
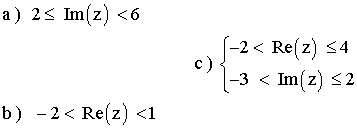
1 ) Representa graficamente donde están situados todos los números complejos cuya parte real vale 3.
2 ) Representa graficamente donde están situados todos los números complejos cuya parte imaginaria vale - 4.
3 ) Representa graficamente los números complejos que tienen la parte real igual a la parte imaginaria.
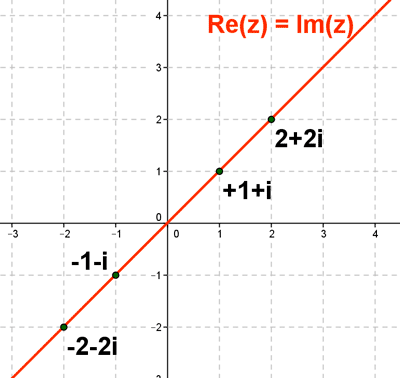
Es la recta y = x
4 ) Representa graficamente los números complejos z tales que:
![]()
a )
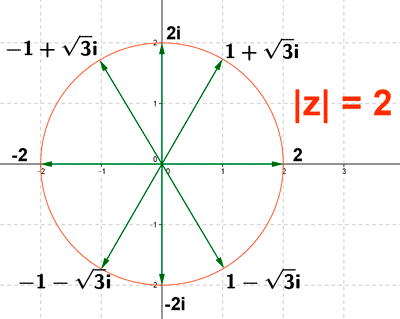
Todos los puntos que están en la circuferencia de centro ( 0,0 ) y de radio 2.
b )

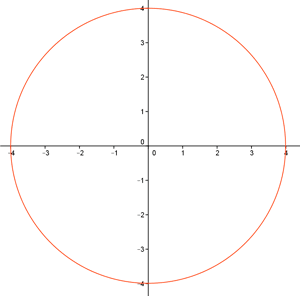
5 ) Representa graficamente los números complejos que cumple:
![]()
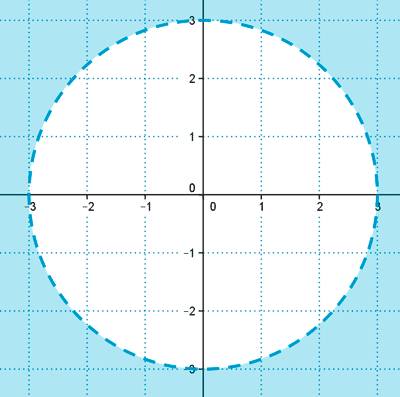
Son los puntos exteriores a la circunferencia de radio 3 y centro (0,0).
![]()
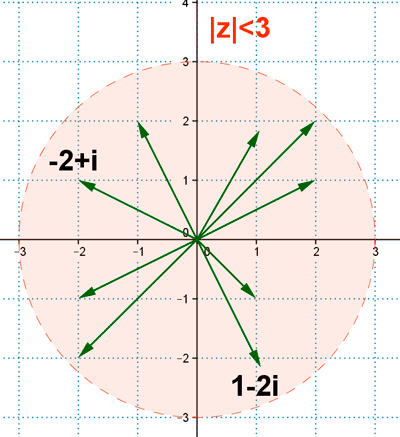
Son los puntos interiores a la circunferencia de radio 3 y centro (0,0).
6 ) Representa graficamente los números complejos que cumple:
![]()
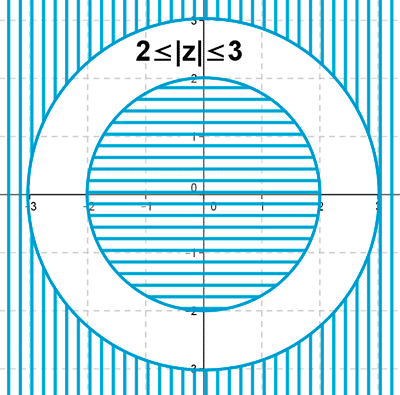
Son los puntos interiores comprendidos entre la circunferencia de radio 2 y la circunferencia de radio 3 es decir los valores interiores de la corona circular.
7 ) Representa graficamente los números complejos cuyo argumento valga 60º
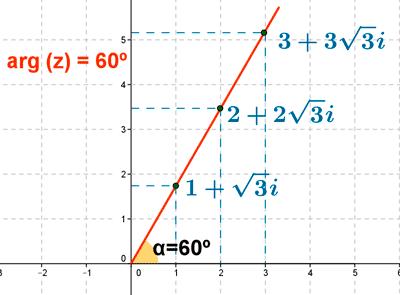
En este caso todos los puntos de la recta del primer cuadrante dibujada en la figura tienen como argumento 60o.
8 ) Representa los números coplejos z tales que:
![]()

Son los números situados en la recta a=-4
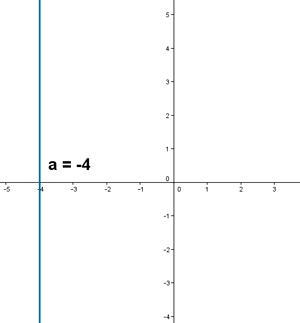
9 ) Representa los números coplejos z tales que:
![]()
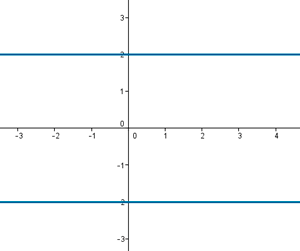
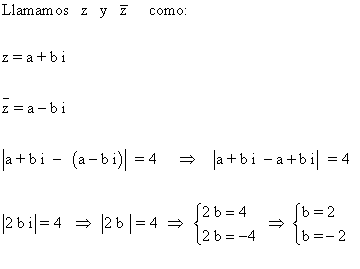
Son los números situados en la recta b = 2 y b = -2
10 ) Representa los números coplejos z tales que:
![]()
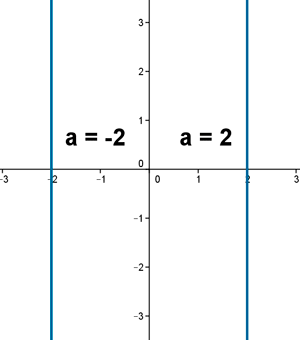
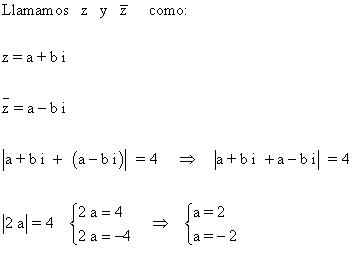
Son los numeros situados en la recta a = -2 y a = 2.
11 ) Representar graficamente las igualdades siguientes. ¿ Qué figura se determina en cada caso ?
![]()
a )
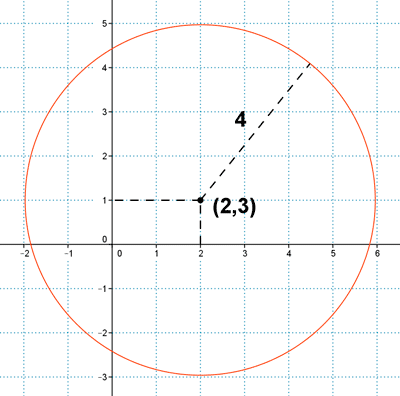
Se cumple en la circunferencia de centro (2,3) y de radio 4.
b )
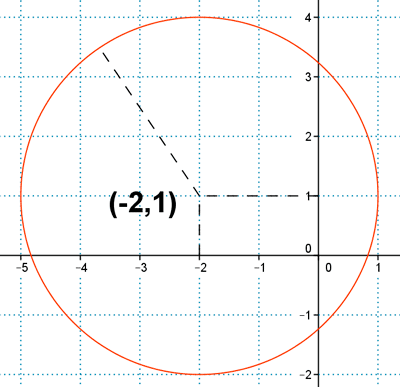
Se cumple en la circunferencia de centro (-2,1) y de radio 3.
12 ) Representa los números coplejos z tales que:
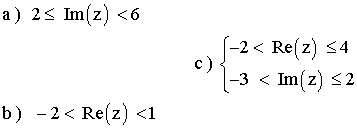
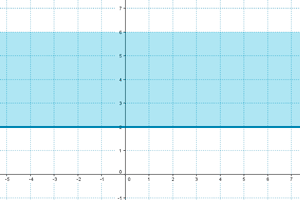
a )
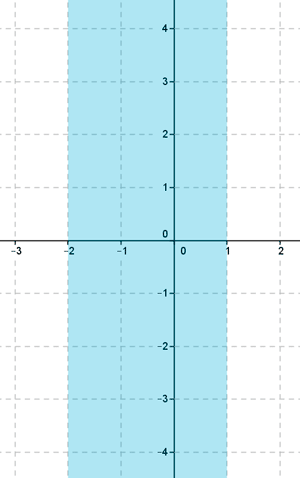
b )
c )


 INICIO
INICIO