Puntos y rectas simétricos
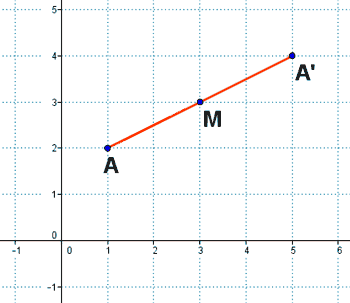
Simetría central
Dado un punto fijo M llamado centro de simetría, los puntos A y A' son simétricos en la simetria central de centro M cuando M es el punto medio del segmento de extremos A y A'
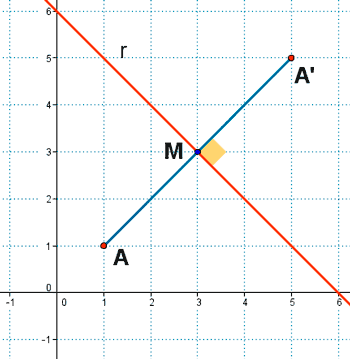
Simetría axial
Dada una recta fija r llamada eje de la simetria, los puntos A y A' son simétricos en la simetria axial de eje r cuando el segmento AA' es perpendicular a r y además el punto de corte de este segmento con el eje es su punto medio M
Ejemplo:
1) Calcula el punto simétrico de A(1, 3) respecto del punto medio M(2, 5)
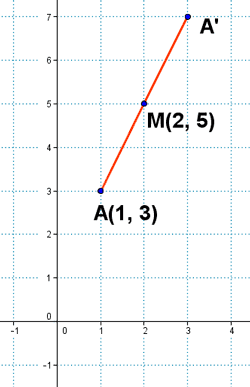
Por definición, el punto M es el punto medio del segmento AA', por lo tanto aplicamos la fórmula conociendo un extremo y el punto medio.:
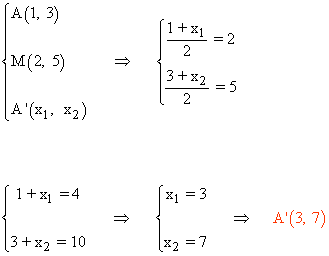
2) Calcula el punto simétrico de A(1, 1) respecto de la recta r: x + y - 6 = 0
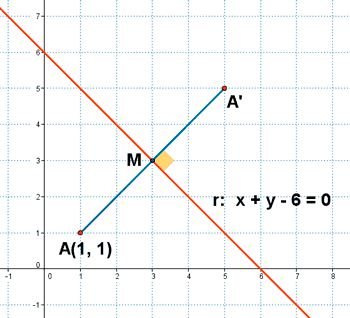
Para calcular el punto simétrico de A(1, 1) , tenemos que calcular una recta s que sea perpendicular a r y que pase por M . Para ello utilizamos el vector normal a la recta r y la ecuación continua de la recta:
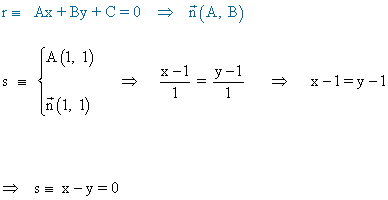
A continuación calculamos el punto M que es la intersección de las dos rectas:
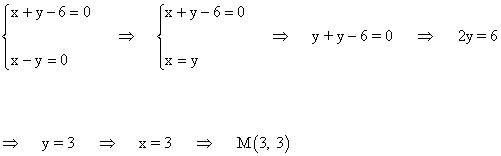
Por último, aplicamos la fórmula del punto medio del segmento AA':
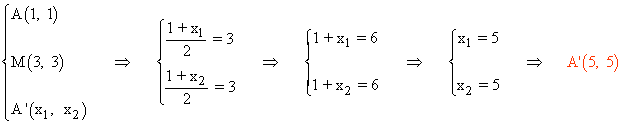
3) Calcula la recta simétrica de r: 3x - y = 0 respecto de la simetría central con centro M(2, -1) .
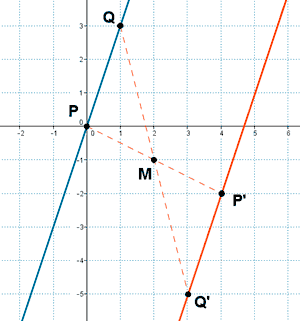
Tomamos dos puntos que pertenezcan a la recta r y se calculan sus puntos simétricos respecto a M(1, 2):
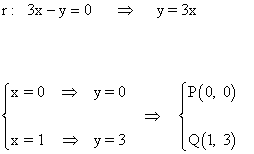
A continuación buscamos dos puntos P' y Q' teniendo en cuenta que M será el punto medio de los segmentos PP' y QQ' :
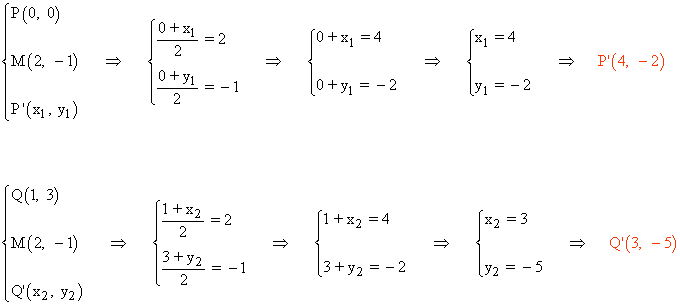
La recta que buscamos es la que pasa por los puntos P' y Q' :
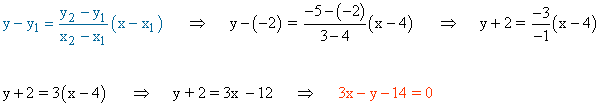


 INICIO
INICIO

