Ejercicios resueltos con ángulos y bisectrices
1 ) Hallar la ecuación de la recta r que pasa por el punto (2, 1) y forma con la recta s: y = 2x - 1 un ángulo de 45º .
2 ) Calcula la distancia del punto P(1, -1) a cada una de las siguientes rectas:
a) r: (x, y) = (1, 3) + t(1, -3) s: {x = 2 + 7t, y= 3t}
b) r: y = 3x - 2 s: 2x - 5y + 3 = 0
c) r: 3x - 2y + 1 = 0 s: 2x - 5y + 3 = 0
d) r: 2x + y - 3 = 0 s: (x + 1)/7 = (y - 1)/4
e) r: x/1 = (y + 3)/2 s: (x - 2)/(-1) = (y + 1)/5
f) r: y = 4x - 2 s: 5x + 3y = 0
3 ) Halla las bisectrices de los ángulos que forman las rectas:
r: 4x - 3y + 9 = 0
s: 12x + 5y - 7 = 0
4 ) Halla las ecuaciones de las rectas que pasan por el punto de intersección de las rectas y = x + 2 y 3x + y = 2 formando un ángulo de 45º con la segunda de ellas.
5 ) Las rectas 2x + 3y - 3 = 0 y ax + y - 5 = 0 forman un ángulo de π/6 rad. ¿Cuánto vale a?
6 ) Dadas las rectas r: 3x + 2y - 2 = 0 y s: 2x - 3y + 1 = 0 , hallar:
a) El ángulo que forman
b) Las ecuaciones de las bisectrices
7 ) La recta r : -7x + 10 y - 1 = 0 es la bisectriz de un ángulo recto cuyo vértice es V ( -3 , -2 ). Halla las ecuaciones de los lados del ángulo.
1 ) Hallar la ecuación de la recta r que pasa por el punto (2, 1) y forma con la recta s: y = 2x - 1 un ángulo de 45º .
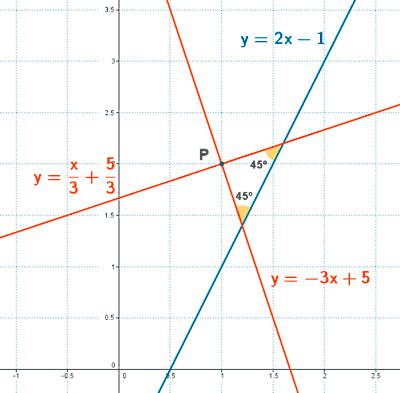
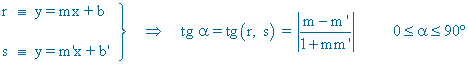
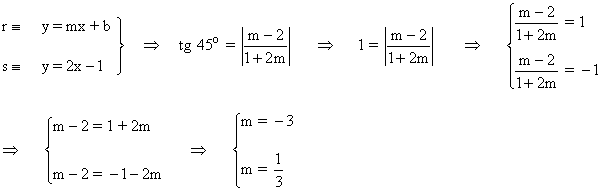
Solo falta aplicar la ecuación punto pendiente que pasa por el punto (2, 1):
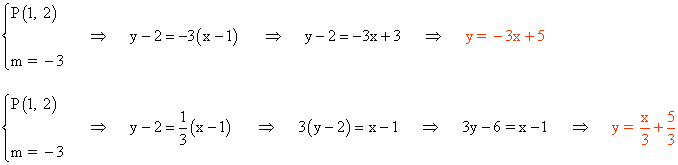
2 ) Calcula la distancia del punto P(1, -1) a cada una de las siguientes rectas:
a) r: (x, y) = (1, 3) + t(1, -3) s: {x = 2 + 7t, y= 3t}
b) r: y = 3x - 2 s: 2x - 5y + 3 = 0
c) r: 3x - 2y + 1 = 0 s: 2x - 5y + 3 = 0
d) r: 2x + y - 3 = 0 s: (x + 1)/7 = (y - 1)/4
e) r: x/1 = (y + 3)/2 s: (x - 2)/(-1) = (y + 1)/5
f) r: y = 4x - 2 s: 5x + 3y = 0
(a)
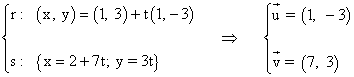
Utilizamos para calcular el ángulo la siguiente fórmula conocidos los vectores directores de ambas rectas:
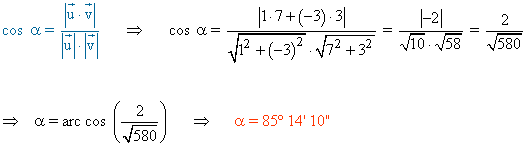
(b)
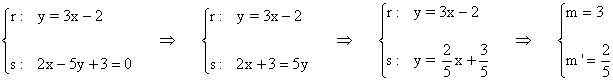
Utilizamos para calcular el ángulo la siguiente fórmula conocidas las pendientes de ambas rectas:
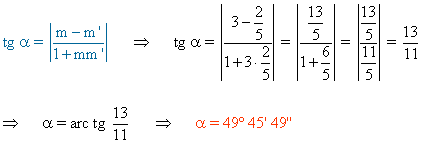
(c)
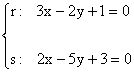
Utilizamos para calcular el ángulo la siguiente fórmula al tener en forma general ambas rectas:
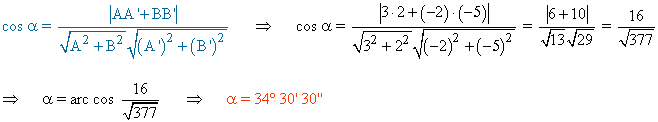
(d)
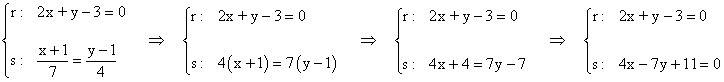
Utilizamos para calcular el ángulo la siguiente fórmula al tener en forma general ambas rectas:
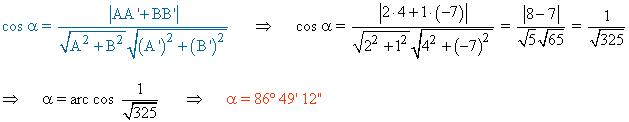
(e)
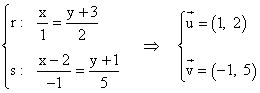
Utilizamos para calcular el ángulo la siguiente fórmula conocidos los vectores directores de ambas rectas:
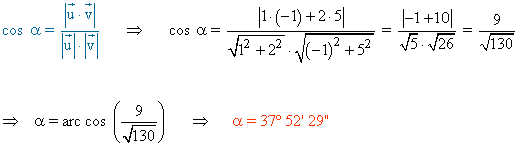
(f)
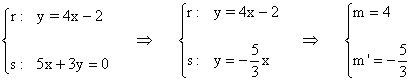
Utilizamos para calcular el ángulo la siguiente fórmula conocidas las pendientes de ambas rectas:
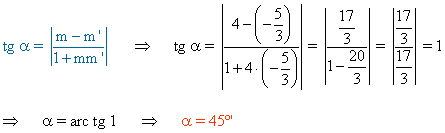
3 ) Halla las bisectrices de los ángulos que forman las rectas:
r: 4x - 3y + 9 = 0
s: 12x + 5y - 7 = 0
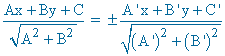
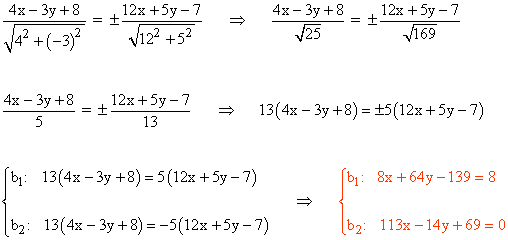
4 ) Halla las ecuaciones de las rectas que pasan por el punto de intersección de las rectas y = x + 2 y 3x + y = 2 formando un ángulo de 45º con la segunda de ellas.
En primer lugar calculamos el punto de corte de las dos rectas:
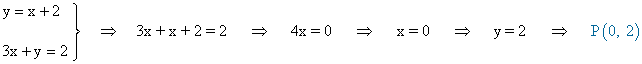
A continuación, conocido el punto de corte, calculamos el ángulo que forma la recta que nos piden con la segunda utilizando la fórmula de la tangente del ángulo que forman dos rectas:
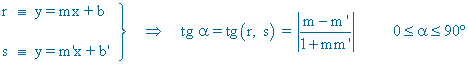
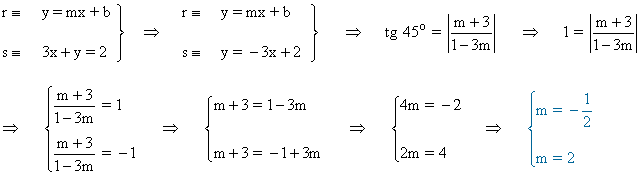
Solo falta aplicar la ecuación punto pendiente que pasa por el punto (0, 2):
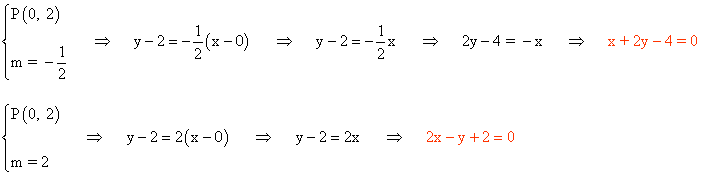
5 ) Las rectas 2x + 3y - 3 = 0 y ax + y - 5 = 0 forman un ángulo de π/6 rad. ¿Cuánto vale a?
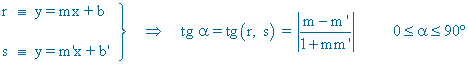
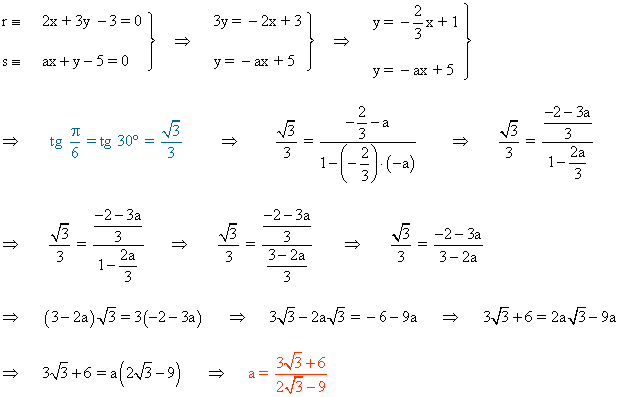
6 ) Dadas las rectas r: 3x + 2y - 2 = 0 y s: 2x - 3y + 1 = 0 , hallar:
a) El ángulo que forman
b) Las ecuaciones de las bisectrices
(a)
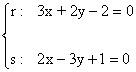
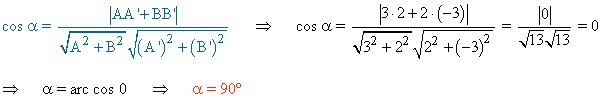
(b)
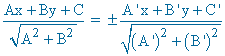
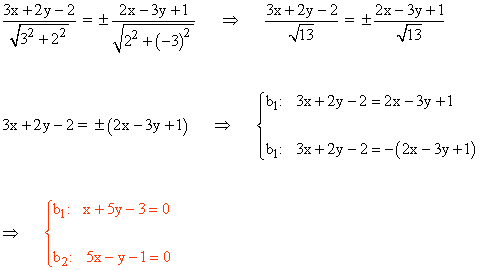
7 ) La recta r : -7x + 10 y - 1 = 0 es la bisectriz de un ángulo recto cuyo vértice es V ( -3 , -2 ). Halla las ecuaciones de los lados del ángulo.
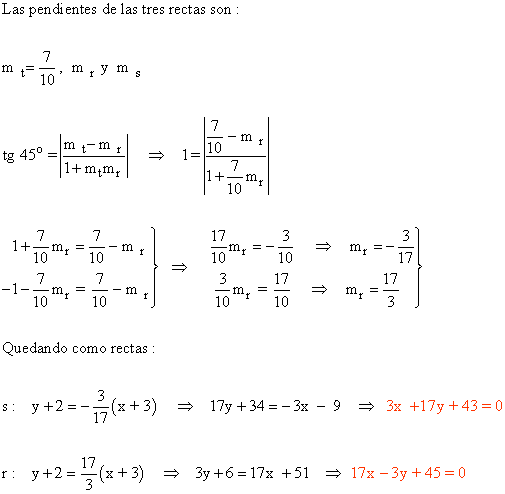
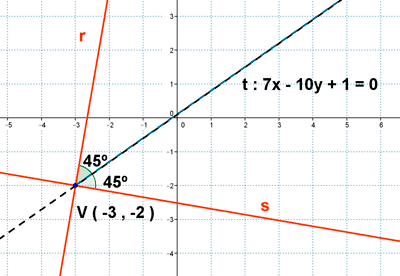


 INICIO
INICIO