Simetría axial.

Una simetría axial de eje e es un movimiento en el plano que convierte un punto A en otro A', de modo que la distancia del eje a ambos puntos es igual y la recta AA' es perpendicular al eje.

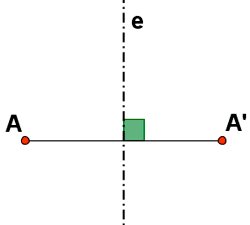
simetria axial de un punto

A partir de la simetría axial de varios puntos, podemos dibujar figuras simétricas de eje e.

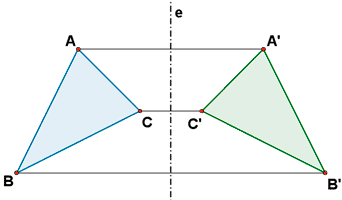
simetria axial de una figura plana

Simetrías respecto a los ejes.

Simetría respecto al eje de ordenadas.

Dos puntos A ( x, y ) y A' ( x', y' ) simétricos respecto del eje de ordenadas tienen sus abcisas opuestas y sus ordenadas iguales.

Las ecuaciones de la simetría respecto del eje OY son :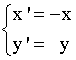

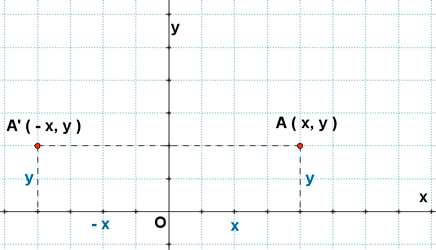
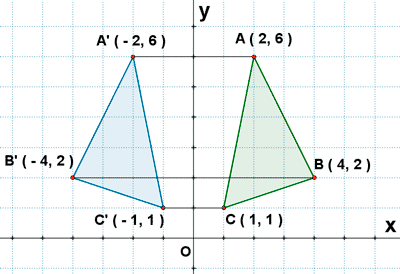
simetria de un punto respecto eje ordenadas simetria figura plana respecto eje ordenadas

Simetría respecto al eje de abcisas.

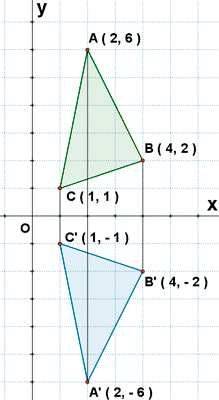
Dos puntos A ( x, y ) y A' ( x', y' ) simétricos respecto del eje de abcisas tienen sus abcisas iguales y sus ordenadas opuestas.

Las ecuaciones de la simetría respecto del eje OX son :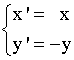

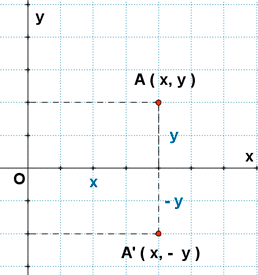
simetria de un punto respecto eje abcisas

simetria figura plana respecto eje abcisas

Propiedades de la simetría axial.

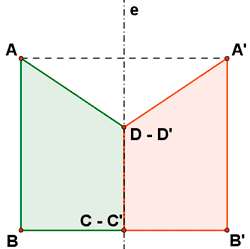
Los puntos del eje de simetría son invariantes, es decir, su homologo son ellos mismo.

Conserva la forma y la distancia. Por tanto, es una transformación isométrica.

El sentido de las figuras no se conserva. Decimos entonces que la simetría axial es un movimiento inverso del plano.

El eje de simetría es la mediatriz de cada uno de los segmentos que une los puntos homólogos.

Dos rectas homólogas se cruzan en un eje de simetría.

Una recta es invariante si esta se transforma en sí misma.