Traslación y dilatación de parábolas.
Traslación horizontal.
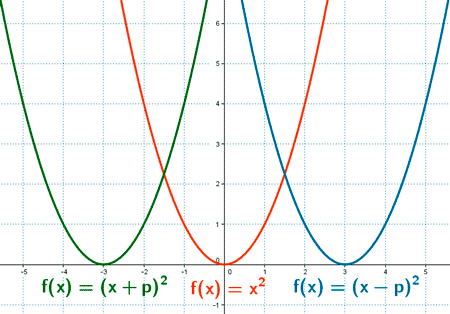
La expresión algebraica de la parábola que resulta de trasladar la parábola f (x) = x 2 horizontalmente es f (x) = (x - p) 2
- Si p > 0, la parábola se desplaza p unidades hacia la derecha.
- Si p < 0, la parábola se desplaza p unidades hacia la izquierda.
El vértice de la parábola se encuentra en el punto ( p, 0 ).
Traslación vertical.
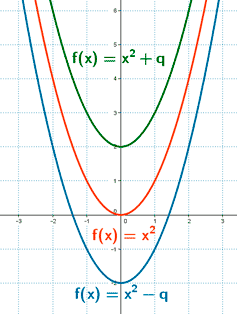
La expresión algebraica de la parábola que resulta de trasladar la parábola f (x) = x 2 verticalmente es f (x) = x 2 + q
- Si q > 0, la parábola se desplaza q unidades hacia arriba.
- Si q < 0, la parábola se desplaza q unidades hacia abajo.
El vértice de la parábola se encuentra en el punto ( 0, q )
Traslación horizontal y vertical.
La expresión algebraica de la parábola que resulta de trasladar la parábola f (x) = x 2 horizontal y verticalmente es f (x) = (x - p) 2 + q
- Si p > 0 y q > 0, la parábola se desplaza p unidades hacia la derecha y q unidades hacia arriba.
- Si p > 0 y q < 0, la parábola se desplaza p unidades hacia la derecha y q unidades hacia abajo.
- Si p < 0 y q > 0, la parábola se desplaza p unidades hacia la izquierda y q unidades hacia arriba.
- Si p < 0 y q < 0, la parábola se desplaza p unidades hacia la izquierda y q unidades hacia abajo.
El vértice de la parábola se encuentra en el punto ( p, q )
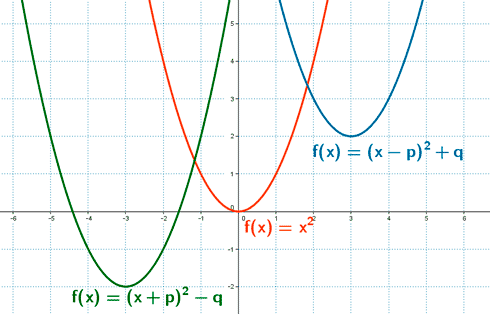
Traslación de parábolas f (x) = ax 2
La expresión algebraica de la parábola que resulta de trasladar la parábola f (x) = ax 2 horizontal y verticalmente es g (x) = a(x - p) 2 + q
Si se traslada la parábola f (x) = ax 2, su ecuación y su gráfica se trasladarán de la misma forma que la función f (x) = x 2
- Si p > 0 y q > 0, la parábola se desplaza p unidades hacia la derecha y q unidades hacia arriba.
- Si p > 0 y q < 0, la parábola se desplaza p unidades hacia la derecha y q unidades hacia abajo.
- Si p < 0 y q > 0, la parábola se desplaza p unidades hacia la izquierda y q unidades hacia arriba.
- Si p < 0 y q < 0, la parábola se desplaza p unidades hacia la izquierda y q unidades hacia abajo.
El vértice de la parábola se encuentra en el punto ( p, q )
Ejemplo 1 :
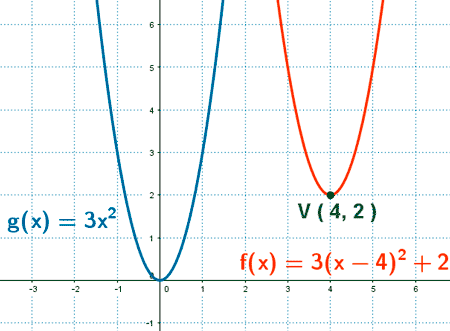
Compara la función f (x) = 3( x - 4 ) 2 + 2 con la función g (x) = 3x 2
La gráfica de la función f (x) = 3( x - 4 ) 2 + 2 resulta de trasladar verticalmente 2 unidades y horizontalmente 4 unidades la gráfica de la función g (x) = 3x 2. El vértice de la función f (x) se encuentra ahora en el punto V ( 4, 2 ).
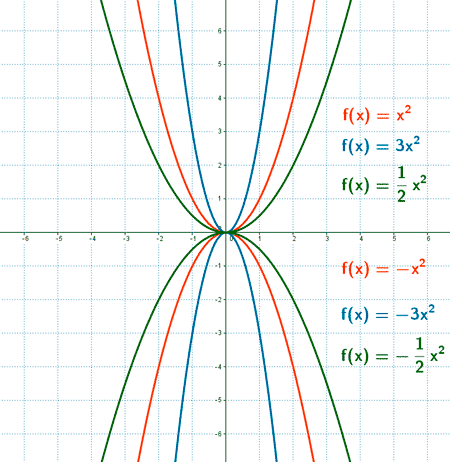
Dilatación de una parábola. Papel del término a del término cuadratico.
La dilatación o apertura de una parábola depende del coeficiente a del término cuadrático de la función. Cuanto mayor es el valor absoluto de a , más cerrada es la parábola.
Ejemplo 2 :
Obtener la expresión algebraica de la parábola siguiente :
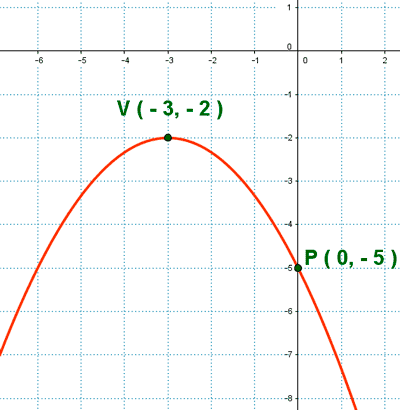
En primer lugar escribimos la expresión algebraica de la parábola, teniendo en cuenta para ello el vértice de la misma.
f (x) = a(x - p) 2 + q → f (x) = a ( x + 3 ) 2 - 2
En segundo lugar tomamos un punto cualquiera de la función, en este caso el punto P ( 0, - 5 ), punto de corte con el eje Y, y lo sustituimos en la expresión algebraica de la función :
f (x) = a ( x + 3 ) 2 - 2 → - 5 = a ( 0 + 3 ) 2 - 2 → - 5 = 9 · a - 2 → a = ![]()
La expresión algebraica de la parábola de la gráfica es :
![]()


 INICIO
INICIO

