Tasa de variación media.
Tasa de variación media en un intervalo.
La tasa de variación media, TVM, de una función, f(x), en un intervalo [x1 , x2], es:
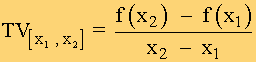
La tasa de variación media en un intervalo es la pendiente de la recta que une los puntos de la gráfica correspondientes a los extremos del intervalo.
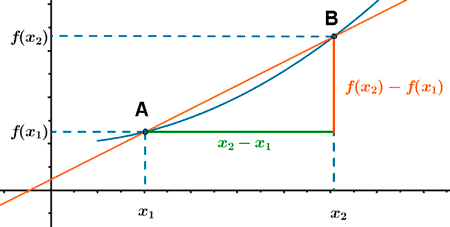
La tasa de variación media de f en el intervalo [ x 1, x 2 ] es la pendiente del segmento AB.
Crecimiento y decrecimiento. Tasa de variación media.
Tasa de variación media en una función estrictamente creciente es mayor que cero.
Si f(x) es estrictamente creciente en el intervalo [x1 , x2], la tasa de variación media (TVM) es estrictamente positiva.
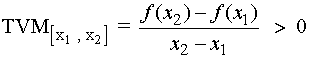
Tasa de variación media en una función estrictamente decreciente es menor que cero.
Si f(x) es estrictamente decreciente en el intervalo [x1 , x2], la tasa de variación media (TVM) es estrictamente negativa.
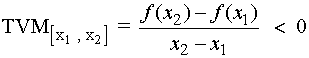
Tasa de variación media en una función constante es igual a cero.
Si f(x) es constante en el intervalo (x1 , x2) , la tasa de variación media en ese intervalo es cero.
Como f(x) es constante en (x1 , x2), entonces:
![]()
Ejemplo de tasa de variación media de una función
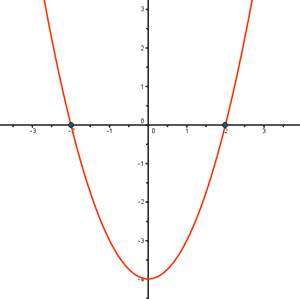
Determina la tasa de variación media de la función f(x) = x2 - 4 en los intervalos: [0 ,2] , [-2 , 2] , [3 , 5]
Aplicamos la definición en cada intervalo pedido:
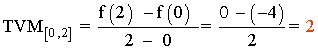
La tasa de variación media en [0 , 2] es positiva,
por lo que la función es creciente.
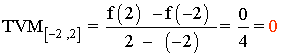
La tasa de variación media en [-2 , 2] es nula,
pero la función no es constante. Los extremos del intervalo coinciden con los puntos de corte de la función con el eje X. Además, en dicho intervalo, la función es tanto creciente como decreciente.
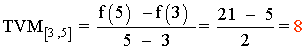
La tasa de variación media en [3 , 5] es positiva,
y la función sí es creciente en dicho intervalo.


 INICIO
INICIO

