Crecimiento y decrecimiento de una función.
Crecimiento y decrecimiento.
Una función es creciente en un intervalo si al aumentar los valores de la variable independiente, aumentan los valores de la variable dependiente.
f es creciente en [ a, b ] si x 1 < x 2 → f ( x 1 ) < f ( x 2 )
Una función es decreciente en un intervalo si al aumentar los valores de la variable independiente, disminuyen los valores de la variable dependiente.
f es decreciente en [ a, b ] si x 1 < x 2 → f ( x 1 ) < f ( x 2 )
Crecimiento y decrecimiento. Máximos y mínimos relativos.
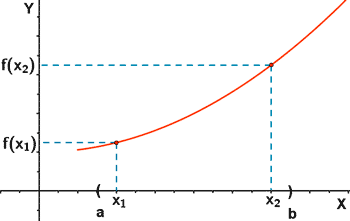
Función estrictamente creciente en el
intervalo ( a, b)
Sea el intervalo ( a, b ) contenido en el dominio
de la función f ( x) y dos valores cualesquiera
x 1 y x 2 tales que x 1 < x 2 :
Si f ( x 1 ) < f ( x 2 ), la función es estrictamente
creciente en el intervalo ( a, b ).
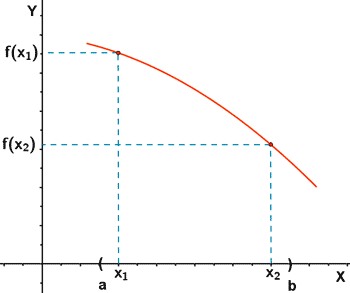
Función estrictamente decreciente en el
intervalo ( a, b)
Sea el intervalo ( a, b ) contenido en el dominio
de la función f ( x) y dos valores cualesquiera x 1 y x 2
tales que x 1 < x 2 :
Si f ( x 1 ) > f ( x 2 ), la función es estrictamente
decreciente en el intervalo ( a, b ).
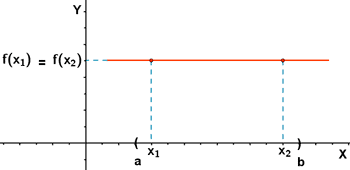
Función constante en el intervalo ( a, b ).
Sea el intervalo ( a, b ) contenido en el dominio
de la función f ( x) y dos valores cualesquiera
x 1 y x 2 tales que x 1 < x 2 :
si f ( x 1 ) = f ( x 2 ), la función es constante en el intervalo ( a, b ).
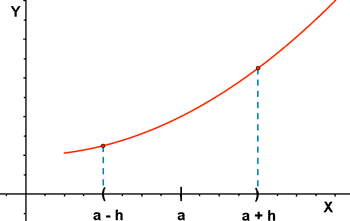
Función estrictamente creciente en x = a.
Una función f ( x ) es estrictamente creciente en x = a si hay un intervalo ( a - h, a + h ) en el que f ( x ) sea estrictamente creciente.
Función estrictamente decreciente en x = a.
Una función f ( x ) es estrictamente decreciente en x = a si hay un intervalo ( a - h, a + h ) en el que f ( x ) sea estrictamente decreciente.
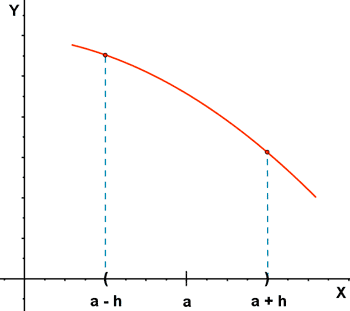
Función que no es estrictamente creciente ni estrictamente decreciente.
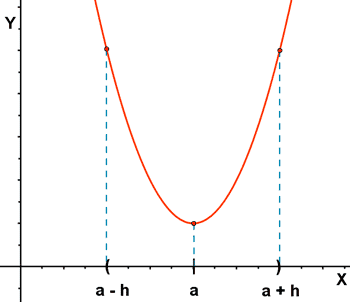
Los extremos relativos de una función son aquellos valores del dominio en los que la función pasa de ser creciente a ser decreciente, o viceversa :
- Si pasa de creciente a decreciente, se denomina máximo relativo.
- Si pasa de decreciente a creciente, se denomina mínimo relativo.
Ejemplo 1 :
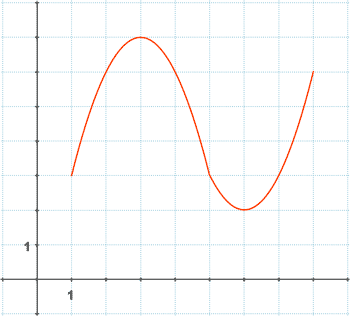
En la gráfica de la función podemos observar como en los intervalos ( 1, 3 ) y ( 6, 8 ), al aumentar el valor de la variable independiente x, también lo hace el valor de la variable dependiente y = f ( x). En este caso, decimos que la función es creciente en esos intervalos.
Por otro lado, en el intervalo ( 3, 6 ), al aumentar el valor de la variable x, disminuye el valor de la variable y = f ( x ). En este caso, diremos que la función es decreciente.


 INICIO
INICIO

