Comparación de integrales similares
Tipo I
![]()
![]()
![]()
![]()
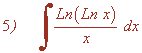
Tipo II
![]()
![]()
![]()
Tipo III
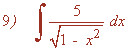
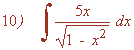
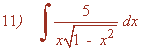
Tipo IV
![]()
![]()
![]()
![]()
Tipo V
![]()
![]()
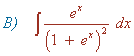
![]()
![]()
![]()
Nota de clase
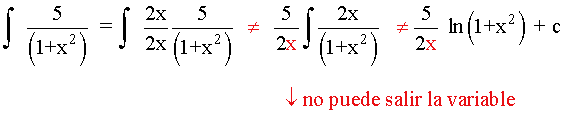
![]()
Esta integral es del tipo logarítmica inmediata.
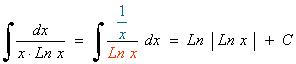
![]()
Esta integral es del tipo potencial inmediata.
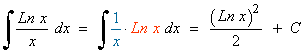
![]()
Esta integral se resuelve por partes.
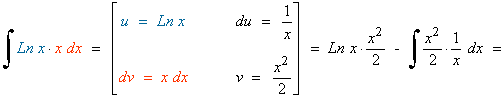
![]()
![]()
Esta integral se resuelve por sustitución o cambio de variable.
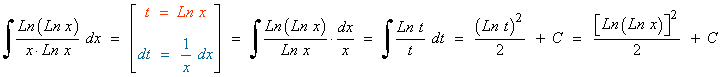
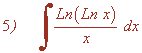
Esta integral se resuelve en primer lugar por sustitución o cambio de variable y despues por partes.
Observamos que el argumento del primer logaritmo es Ln x , y la derivada de éste es 1/x , que también aparece en la integral. Por tanto, si hacemos un cambio de variable la integral quedará más sencilla:
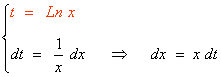
![]()
Como no sabemos integrar el logaritmo, aplicamos integración por partes de tipo II:
![]()
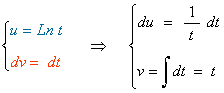
![]()
Deshacemos el cambio, es decir, escribimos t = Ln x :
![]()
![]()
Esta integral es del tipo arcotangente.
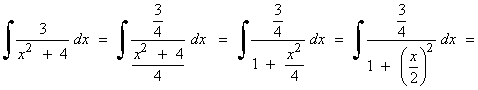
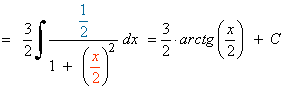
![]()
Esta integral es del tipo logarítmica.
![]()
![]()
Esta integral es del tipo racional.
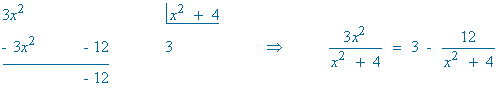
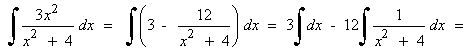
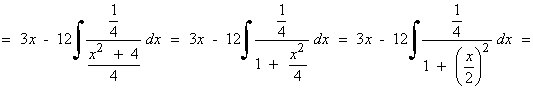
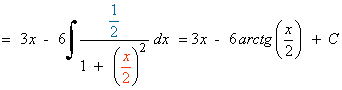
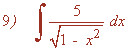
Esta integral es de tipo trigonométrica inversa.
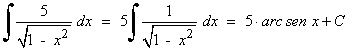
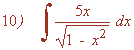
Esta integral es de tipo potencial.
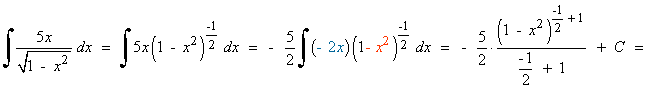
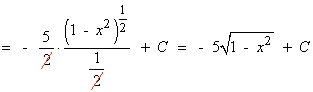
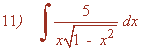
La integral se transforma para aplicar la fórmula, por tanto no es un cambio de variable.
También se puede hacer por sustitución trigonométrica.
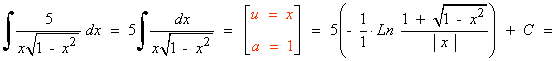
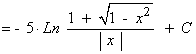
![]()
Esta integral es del tipo potencial.
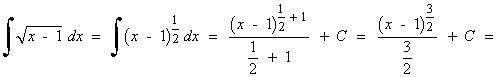
![]()
![]()
Esta integral se resuelve por sustitución o cambio de variable.
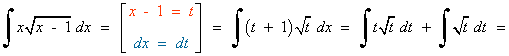
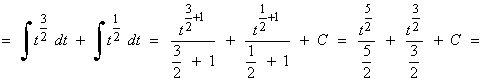
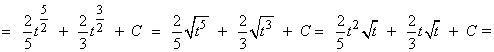
![]()
![]()
Esta integral se resuelve por sustitución o cambio de variable.
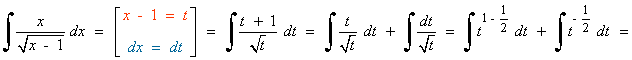
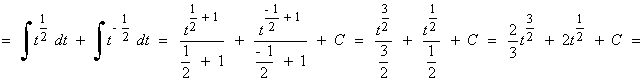
![]()
![]()
![]()
Esta integral se resuelve por sustitución o cambio de variable.
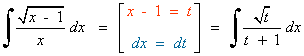
Al realizar la sustitución o cambio de variable, observamos que no se puede descomponer en sumandos.
![]()
Se pueden separar los numeradores pero no los denominadores
Por lo tanto realizamos otro cambio de variable: x - 1 = t2
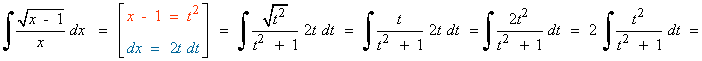
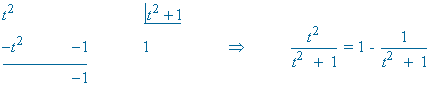
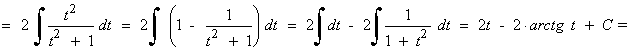
![]()
![]()
![]()
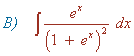
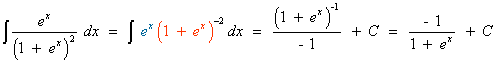
![]()
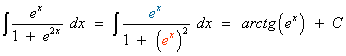
![]()
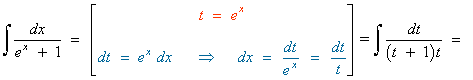
![]()
![]()
![]()
![]()
![]()
![]()
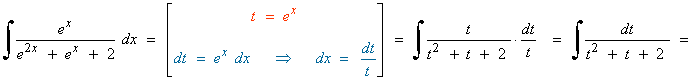
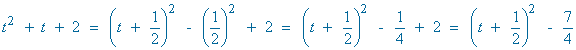
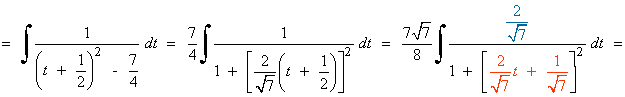
![]()


 INICIO
INICIO