Ejercicios de integrales de funciones racionales de seno y coseno
Tipo I
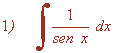
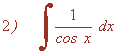
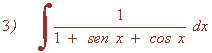
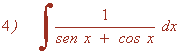
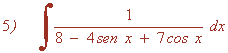
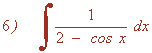
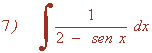
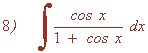
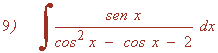
Tipo II
![]()
![]()
![]()
Resuelve las siguientes integrales aplicando sustitución:
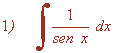
Hacemos el siguiente cambio de variable y sustituimos en la integral:
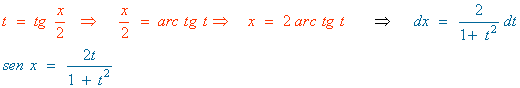
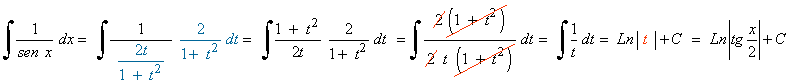
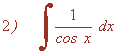
Hacemos el siguiente cambio de variable y sustituimos en la integral:
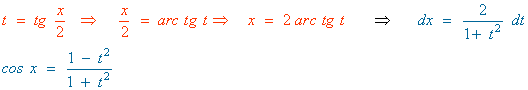
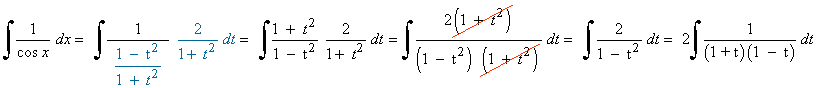
La nueva integral es una integral racional con dos raices reales simples en el denominador:
t1= -1 , t2= 1
Ver integrales racionales.
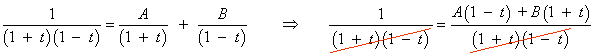
![]()
Para t = -1 : 1 = 2A ⇒ A = 1/2
Para t = 1 : 1 = 2B ⇒ B = 1/2
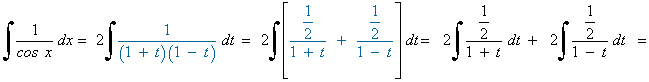
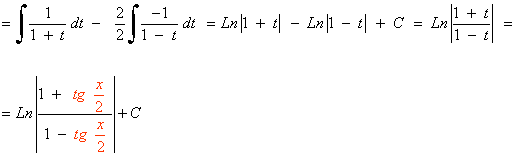
SELECTIVIDAD
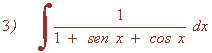
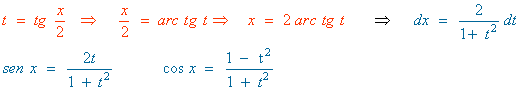
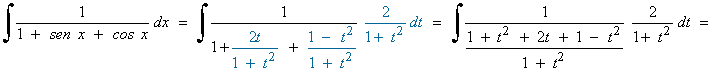
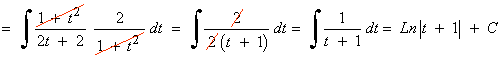
SELECTIVIDAD
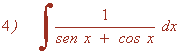
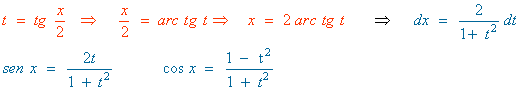
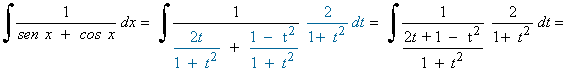
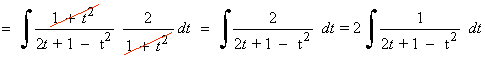
La nueva integral es una integral racional con dos raices reales simples en el denominador:
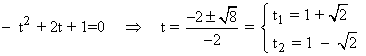
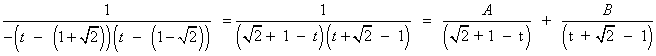
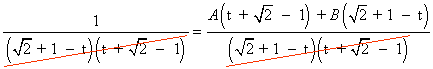
![]()
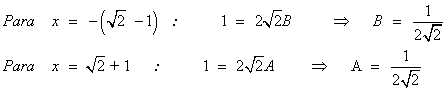
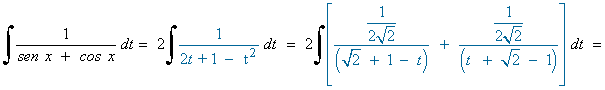
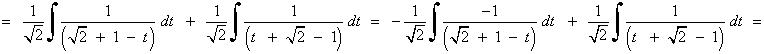
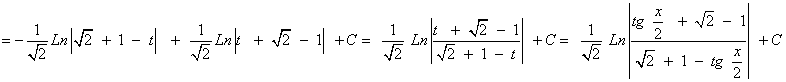
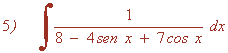
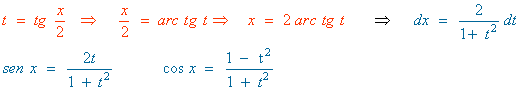
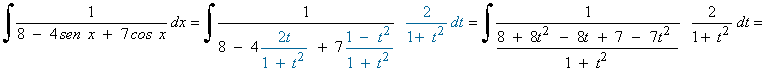
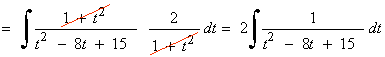
La nueva integral es una integral racional con dos raices reales simples en el denominador:
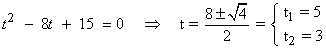
![]()
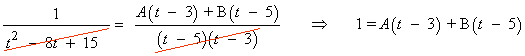
Para t = 5 : 1 = 2A ⇒ A = 1/2
Para t = 3 : 1 = -2B ⇒ B = -1/2
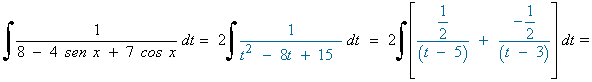
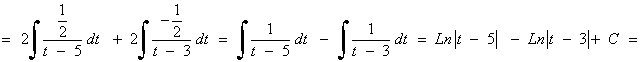
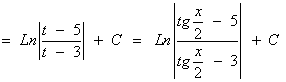
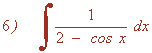
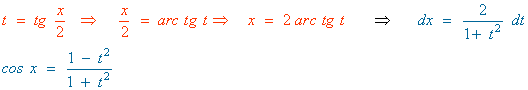
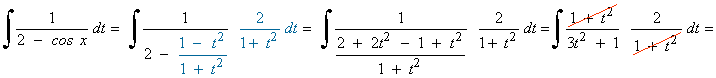
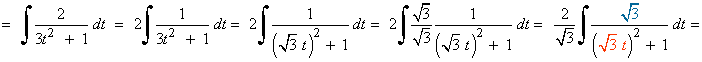
![]()
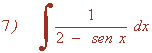
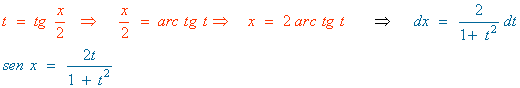
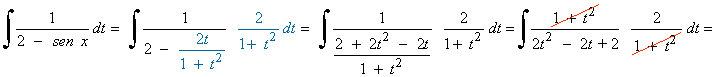
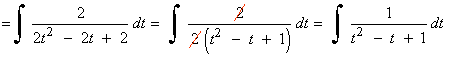
Es una integral racional con raices imaginarias en el denominador, por tanto vamos a resolverla por completación de cuadrados:
![]()
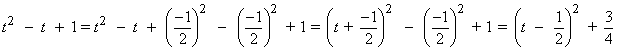
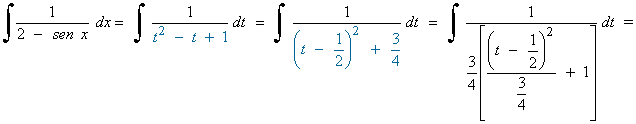
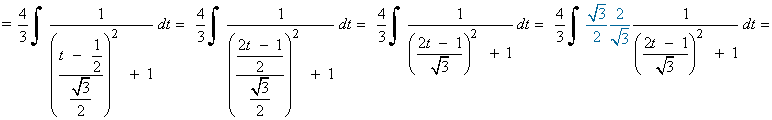
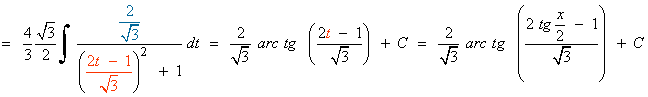
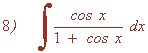
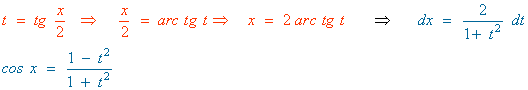
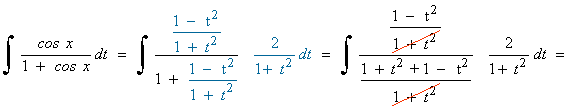
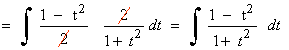
Es una integral racional con grado del numerador mayor que el del denominador, por tanto:
Ver integrales racionales.
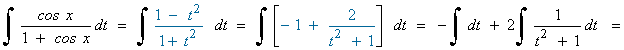
![]()
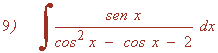
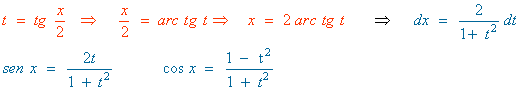
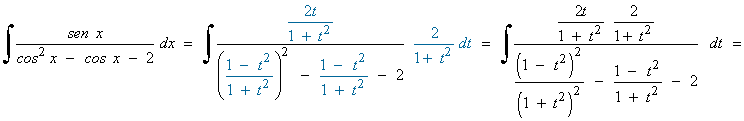
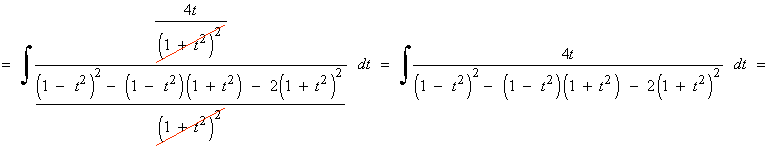
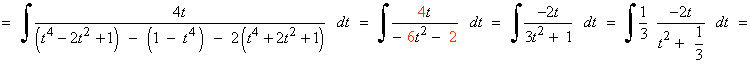
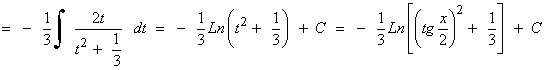
![]()
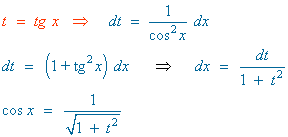
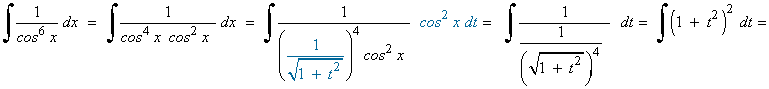
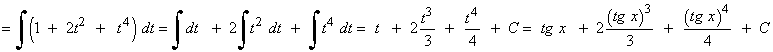
![]()
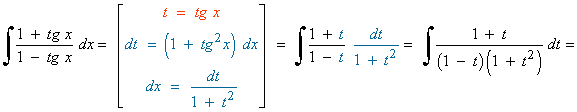
Se trata de una integral racional con una raiz real y dos imaginarias en el denominador.
Por tanto, la descomposición queda:
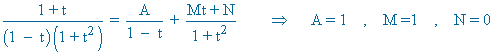
![]()
![]()
![]()
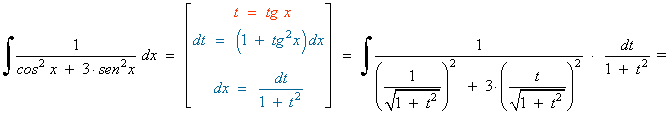
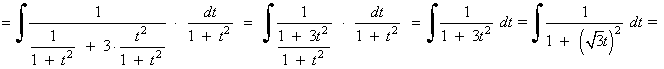


 INICIO
INICIO