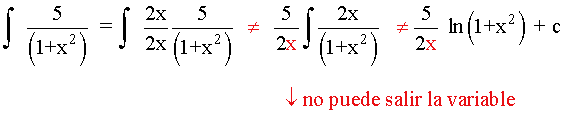Ejercicios de integrales de funciones irracionales
Haga click en la correspondiente pestaña para ver la solución del ejercicio
Tipo I
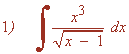
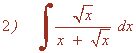
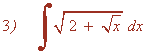
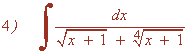
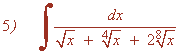
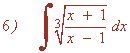
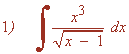
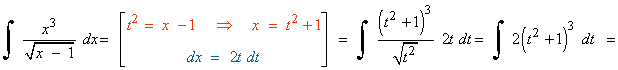
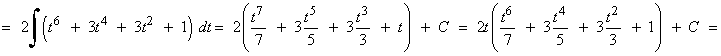
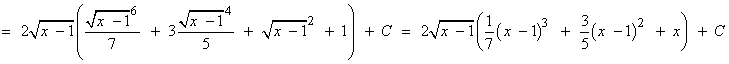
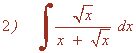
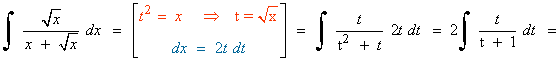
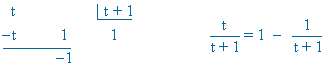
![]()
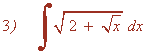
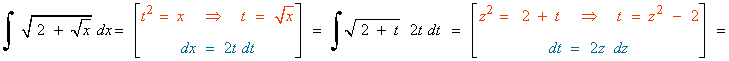
![]()
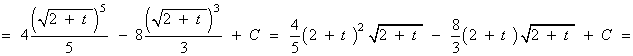
![]()
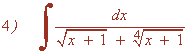
Calculamos el m.c.m. de los índices de las raices: m.c.m.(2 , 4) = 4
Hacemos el cambio de variable: t4 = x + 1
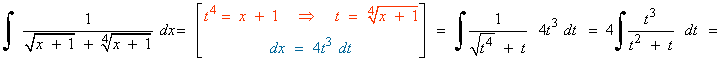
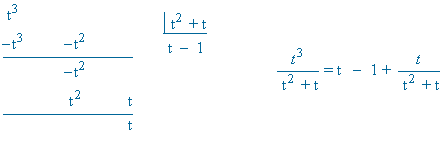
![]()
Para deshacer el cambio necesitamos despejar t2 y t :
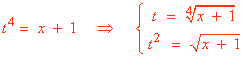
![]()
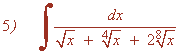
Calculamos el m.c.m. de los índices de las raices: m.c.m.(2 , 4 , 8) = 8
Hacemos el cambio de variable: t8 = x
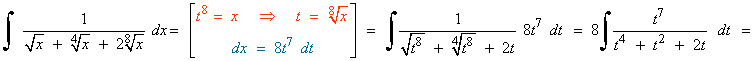
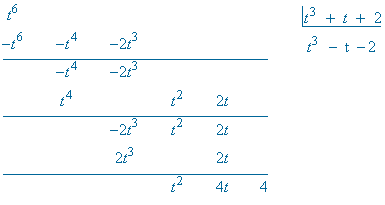
![]()
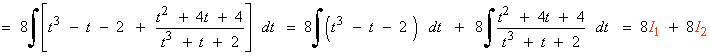
La primera integral I1 es inmediata. La segunda, I2 , es una integral de una función racional.
Vamos a resolver la segunda por separado:
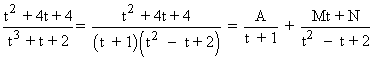
Identificando coeficientes se obtiene:
![]()
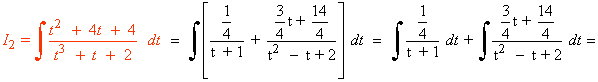
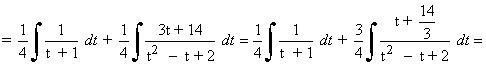
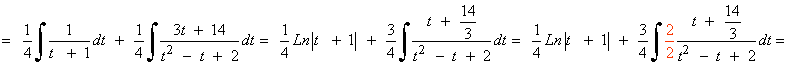
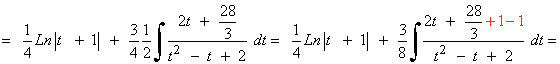
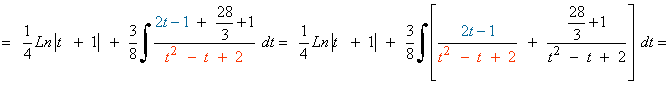
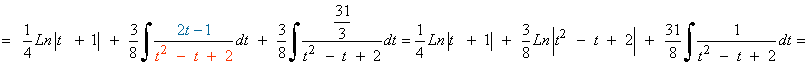
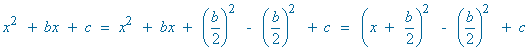
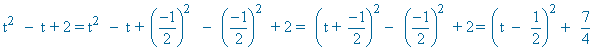
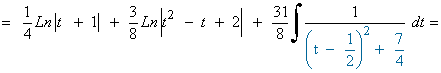
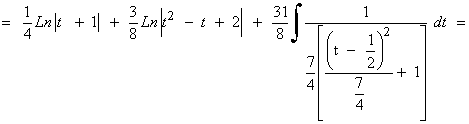
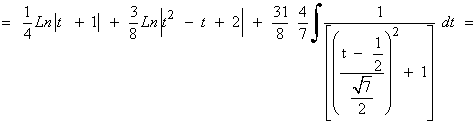
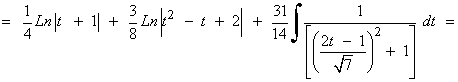
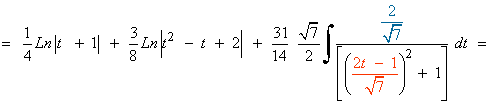
![]()
Solución del ejercicio:
![]()
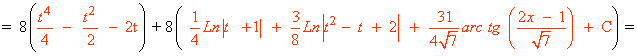
![]()
Para deshacer el cambio necesitamos despejar t , t2 , t4 :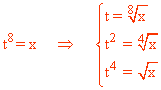
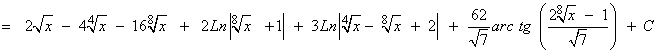
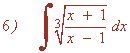
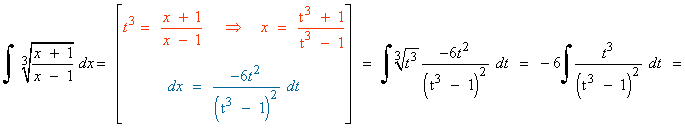
Se trata de una integral de una función racional, por tanto la resolveremos factorizando el denominador y descomponiendo la integral:
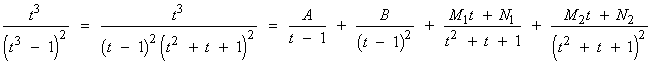
Desarrollando la expresión anterior e identificando los coeficientes de t3 , t2 y t se obtiene el siguiente sistema de ecuaciones:
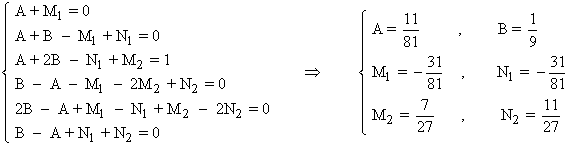
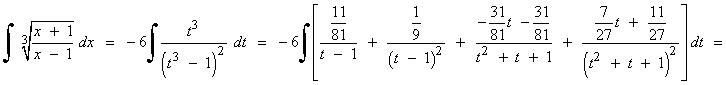
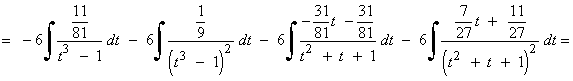
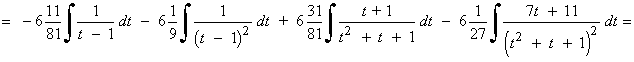
La primera integral se resuelve con la regla del logaritmo, y la segunda, con la regla de la potencia.
La tercera y cuarta, se descomponen en dos nuevas integrales cada una, las cuales se resuelven mediante la regla de la potencia y de la arcotangente.
Simplificando los resultados se deberá obtener el siguiente resultado:
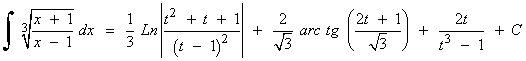
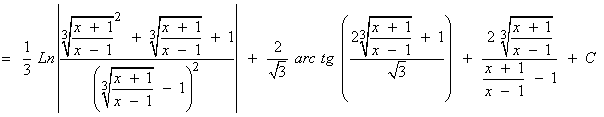


 INICIO
INICIO