Área bajo una curva. Integral definida
Trapecio mixtilíneo
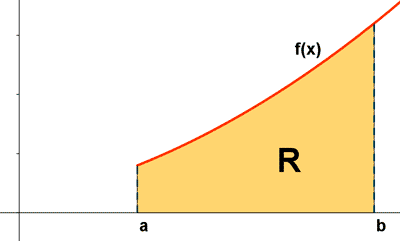
Es la figura determinada por la curva y = f(x) el eje OX y las rectas x = a y x = b .
Partición de un intervalo
Una partición P de un intervalo [a, b] es una colección finita de puntos de [a, b] , donde:
![]()
![]()
Una partición de n+1 puntos divide un intervalo en n subintervalos de [a,b] :
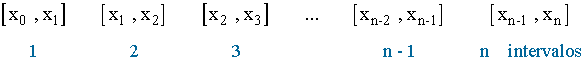
Una partición P es más fina que otra P' cuando P contiene a P' , es decir P' ⊂ P
Son particiones de [-1, 5] : P = {-1, 0, 1, 2, 3, 4, 5}
P' = {-1, 0, 1, 3, 5}
Por lo tanto tenemos que P' ⊂ P
Por el teorema de Weirstrass sabemos que si una función f(x) es continua en el intervalo [a, b] , existen dos puntos de dicho intervalo en los que f(x) alcanza el máximo y el mínimo.
Llamaremos M al valor máximo y m al valor mínimo.
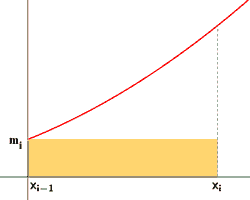
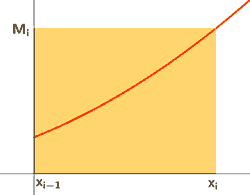
Aplicando el teorema de Weierstrass a cada subintervalo [xi-1, xi], se alcanzan tanto el máximo como el mínimo en dichos subintervalos. Llamaremos Mi al máximo de la función en el intervalo [xi-1, xi] y mi al mínimo de la función en el intervalo [xi-1, xi].
Dado el subintervalo [xi-1, xi] , el valor del producto mi·(xi - xi-1) es el área R del rectángulo contenido en el trapecio mixtilíneo y Mi·(xi - xi-1) es el área del rectángulo que lo contiene.
La suma inferior de f asociada a la partición P es :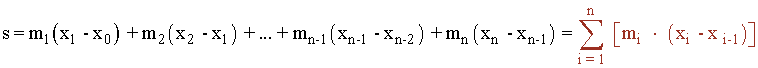
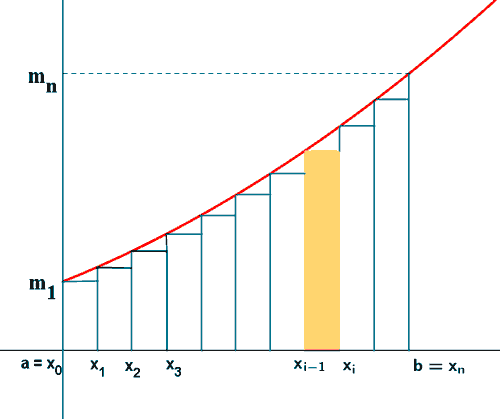
La suma superior de f asociada a la partición P es :
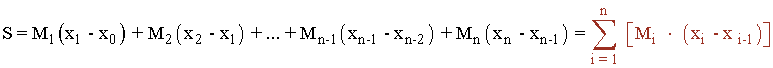
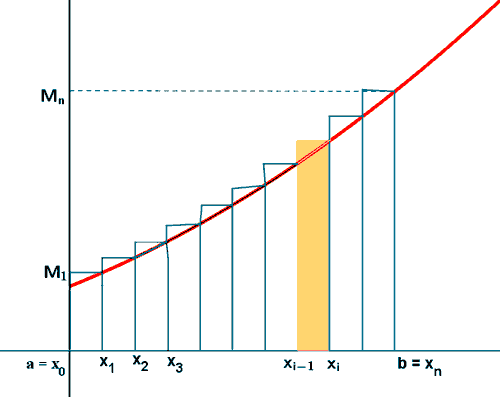
Si llamamos A al área de la región del trapecio mixtilíneo , entonces A está comprendido entre la suma inferior y la suma superior.
Si tomamos particiones cada vez más finas del intervalo llegamos a una sucesión de sumas inferiores creciente y acotada superiormente por cualquiera de las sumas superiores y también una sucesión de sumas superiores decreciente y acotada inferiormente por cualquiera de las sumas inferiores, y en los dos casos por A. Es decir:
![]()
De esta forma, ambas sucesiones tienen límite y al tratarse en nuestro caso de una función continua, el límite coincide:
![]()
Integral definida de una función continua
Dada una función f(x) continua en [a, b] , llamamos integral definida de f(x) en [a, b] al límite común de las sumas superiores e inferiores y lo llamamos de la siguiente forma:
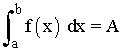
![]()
Esta notación se debe a Leibniz. El símbolo de integral es una S alargada que recuerda que la integral es un límite de suma.

Por tanto, se define el área del trapecio mixtilíneo que delimita la curva de una función continua f(x) y el eje OX entre las rectas x = a y x = b como :
![]()
Toda función que cumpla este requisito, sea continua o no, es Riemann integrable.
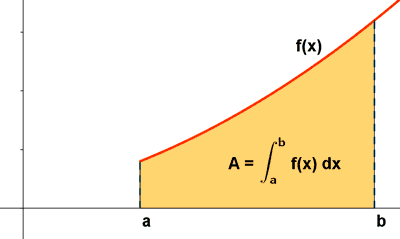
Hallar, aplicando la definción de integral, el área de la región delimitada por la recta f ( x ) = x y el eje de abscisas entre las rectas x = 0 y x = 1.
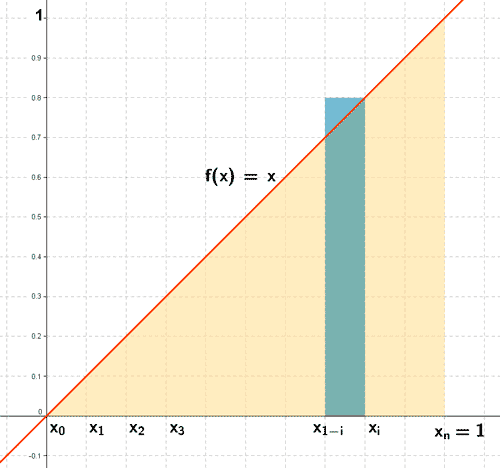
Vamos a tomar la partición del intervalo [0,1] que lo divide en n partes iguales. Sea
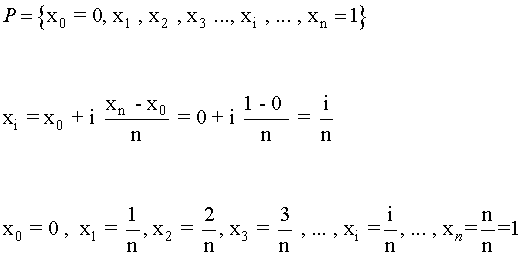
Cada intervalo de la partición tendrá una amplitud de 1/n:
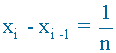
Como la función f(x)=x es creciente, tenemos que, en cada intervalo [ xi-1 , xi ] de la partición se verifica que:
![]()
Teniendo en cuenta todo esto,
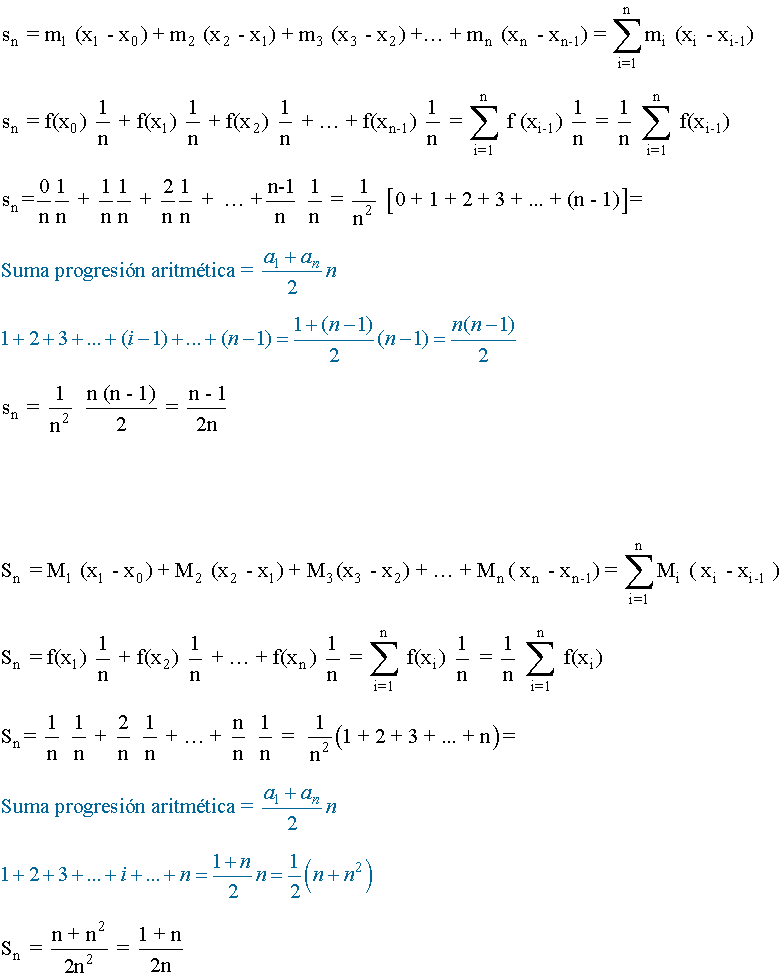
De manera que, los límites de las sumas superiores e inferiores son:

Ambos límites son iguales:
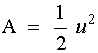
Como f(x) = x es una función integrable en [ 0, 1 ], podemos afirmar que:
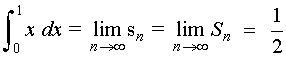
Suma de Riemann animada
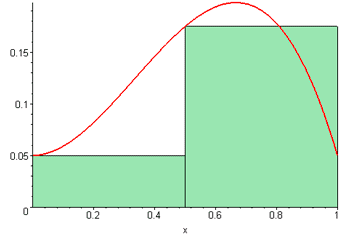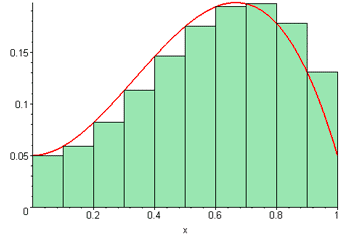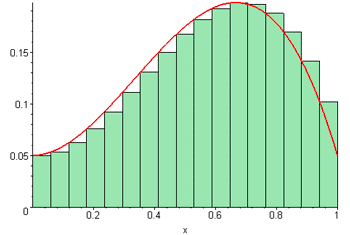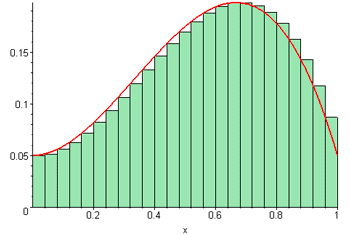
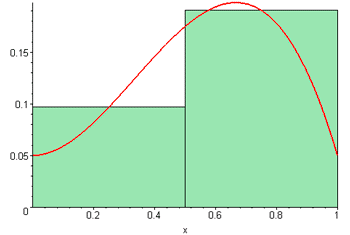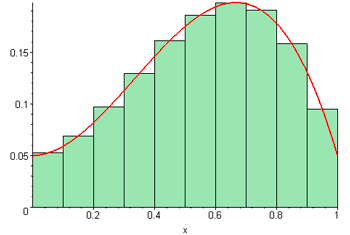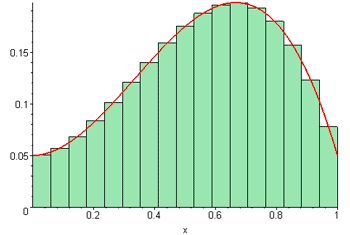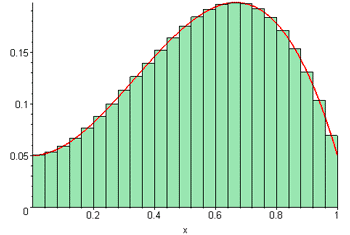
http://commons.wikimedia.org/wiki/Category:Animations_of_curves


 INICIO
INICIO

