Aplicación de la integral definida
al cálculo de áreas de figuras planas
Área delimitada por una curva y = f(x) y el eje de abscisas
CASO I : La función f(x) es positiva en el intervalo [a, b]
Hallar por integración el área del triángulo formado por la bisectriz del primer cuadrante al eje OX y la recta x = 4 . Comparar el resultado con el que se obtiene geométricamente.
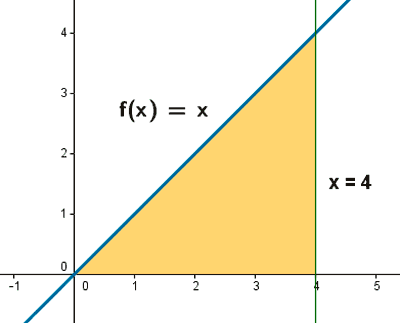
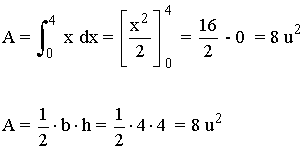
El valor de la integral definida entre los valores x = 0 y x = 4 es el área encerrada bajo la curva:
CASO II : La función f(x) es negativa en el intervalo [a, b]
Hallar el área del recinto limitado por la parábola de la ecuación y = - x2 , el eje OX y las rectas x = 2 y x = 4 .
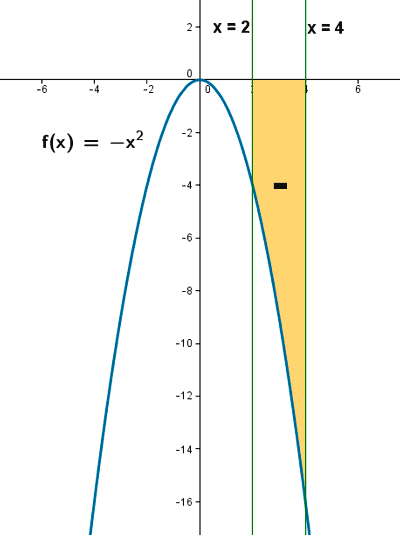
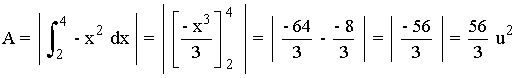
El valor de la integral definida entre los valores x = 2 y x = 4 es el área encerrada bajo la curva pero cambiada de signo. Es por esta razón por la que se toma el valor absoluto.
CASO III : La función f(x) cambia de signo en el intervalo [a, b]
Hallar por integración el área limitada por el eje OX, la curva y = x2 - 4 y las rectas x = 0 y x = 4 .
En primer lugar calculamos los puntos de corte con el eje OX de la función:

A continuación estudiamos el signo de la función en cada uno de los intervalos o se dibuja la gráfica de la función:
| Intervalo | (- ∞, -2) | (-2, 2) | (2, +∞) |
|---|---|---|---|
| Punto de prueba | f(-3) > 0 | f(0) < 0 | f(3) > 0 |
| Signo de f(x) | + | - | + |
Como la función entre 0 y 2 es negativa y de 2 a 4 es positiva, hay un recinto que es negativo (de 0 y 2) y otro positivo (de 2 a 4) :
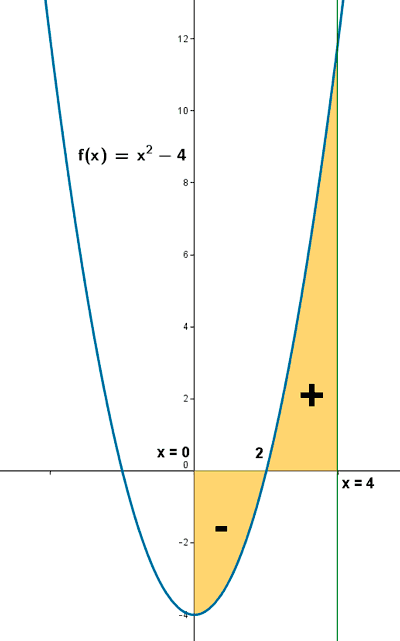
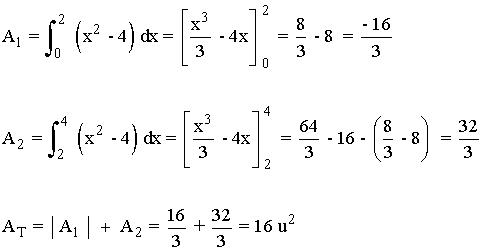
El área es la suma algebráica de las áreas encerradas por la gráfica y el eje OX entre los valores 0 y 4 .


 INICIO
INICIO

