Funciones racionales
Una función es racional si es el cociente de dos polinomios:
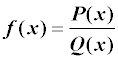
siendo el grado del polinomio Q(x) distinto de 0.
Las características generales de las funciones racionales son:
1) El dominio de las funciones racionales son los números reales menos las raíces del denominador, es decir:
![]()
2) Son discontinuas en los valores de x que son raíces del denominador.
3) Tienen asíntotas verticales en cada raíz del denominador que no lo sea del numerador, y pueden tener asíntotas horizontales y oblicuas.
Función de proporcionalidad inversa
Una función de proporcionalidad inversa es una función racional del tipo:
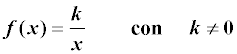
Su gráfica es una hipérbola.
Las características generales de las funciones de proporcionalidad inversa son:
1) El dominio de la función de proporcionalidad inversa es R - {0} .
2) La función es discontinua en x = 0 .
3) En x = 0 existe una asíntota vertical.
4) A medida que los valores de x crecen o decrecen, la función se acerca al eje Y, por lo tanto tiene una asíntota horizontal en y = 0 .
5) La gráfica de este tipo de funciones no corta a los ejes de coordenadas.
6) La función es impar y por tanto simétrica al origen de coordenadas.
7) Para k > 0 la función es decreciente y la gráfica está en el primer y tercer cuadrante.
Para k < 0 la función es creciente y la gráfica está en el segundo y cuarto cuadrante.
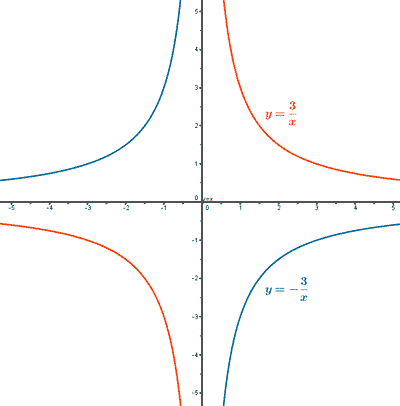
Representación gráfica de funciones de proporcionalidad inversa:
![]()
1) Puntos de corte con los ejes:
Para x = 0 la función f(x) no está definida puesto que f(0) = 3/0 (no real).
Para x = 0 la función g(x) no está definida puesto que g(0) = - 3/0 (no real).
2) Simetrías:
Las funciones f(x) y g(x) son impares, es decir, son simétricas respecto al eje de coordenadas.
![]()
![]()
3) Crecimiento o decrecimiento:
Para la función f(x) tenemos que k > 0 , por lo tanto la función es decreciente y la gráfica está en el primer y tercer cuadrante. Es decir, la función es decreciente en (- ∞, 0) ∪ (0, + ∞).
Para la función g(x) tenemos que k < 0 , por lo tanto la función es creciente y la gráfica está en el segundo y cuarto cuadrante. Es decir, la función es creciente en (- ∞, 0) ∪ (0, + ∞).
4) Tabla de valores:
Construimos una tabla de valores.
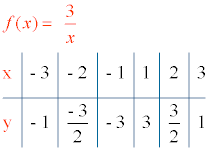
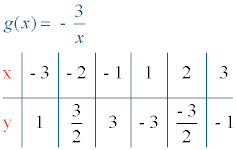


 INICIO
INICIO

