Función inyectiva
Una función f de dominio D = Dom(f) es inyectiva cuando a elementos distintos de D le corresponden imágenes distintas:
Si x1, x2 ∈ D : x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Dos elementos distintos del dominio D no pueden tener la misma imagen.
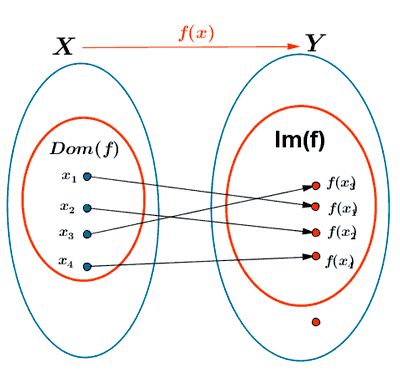
Ejemplo de función inyectiva
a) Veamos si la función f(x) = 4x - 1 es inyectiva:
Si las imágenes son iguales:
f(x1) = f(x2) ⇒ 4x1 - 1 = 4x2 - 1 ⇒ 4x1 = 4x2 ⇒ x1 = x2
, los originales son iguales.
Por tanto, la función f es inyectiva.
Criterio de la recta horizontal
una función es inyectiva si ninguna recta horizontal corta a su gráfica en más de un punto.
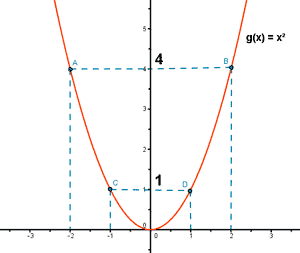
b) Veamos si g(x) = x2 es inyectiva:
Si trazamos rectas horizontales sobre la gráfica,
éstas la corta en más de un punto.
Por ejemplo: si trazamos la recta y = 4 :
ésta corta la función en los puntos: x = 2 , x = -2
g(2) = 4 , g(-2) = 4
Por tanto, dos elementos distintos, 2 y - 2, tienen la misma imagen.
La función g no es inyectiva.
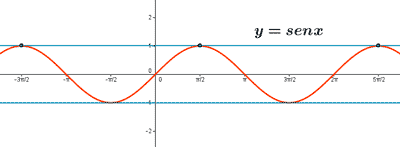
c) Veamos si h(x) = sen x es inyectiva:
Si trazamos rectas horizontales sobre la gráfica,
éstas la corta en más de un punto.
Por ejemplo: si trazamos la recta y = 1 :
ésta corta la función en los puntos: x = π/2 , -3π/2
h(π/2) = 1 , h(-3π/2) = 1
Por tanto, dos elementos distintos, π/2 y -3π/2,
tienen la misma imagen.
La función h no es inyectiva.
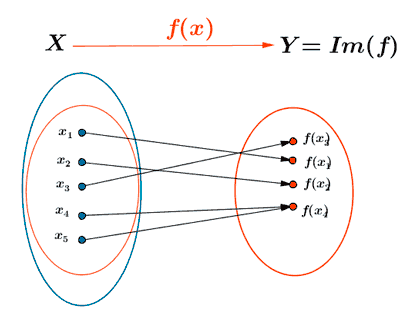
Función sobreyectiva
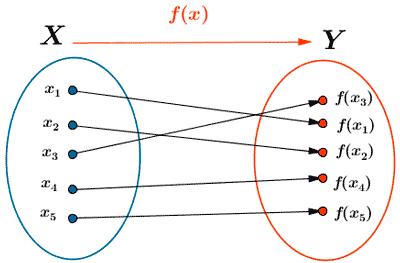
Una función f: X → Y es una función sobreyectiva si:
Im(f) =Y
Esto significa que todo elemento y ∈ Y es la imagen de al menos un elemento x ∈ A . Es decir, la imagen de f coincide con el conjunto final.
Función biyectiva
Una función f es biyectiva si es a la vez inyectiva y sobreyectiva.


 INICIO
INICIO

