Ejercicios resueltos de triángulos cualesquiera II:
Puntos inaccesibles y problemas geométricos
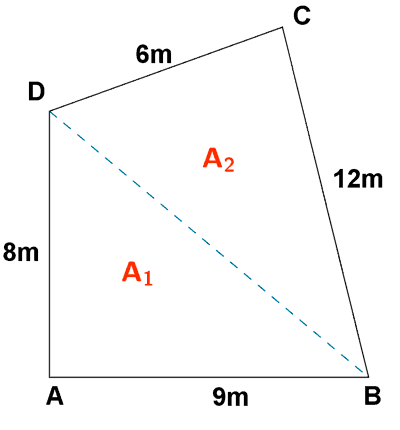
1) Encuentra la superficie de una parcela que tiene forma de cuadrilátero como la figura, en el que se conocen las siguientes medidas:
a) Lados: AB = 9 m BC = 12 m CD = 6 m AD = 8 m
b) Diagonal: BD = 15 m
2) Calcular los lados de un paralelogramo cuyas diagonales miden 6 cm y 5 cm y el ángulo que forma es de 35o 42' 32''
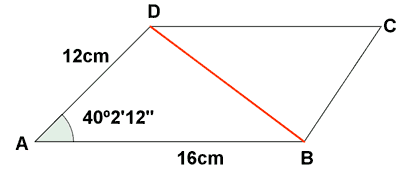
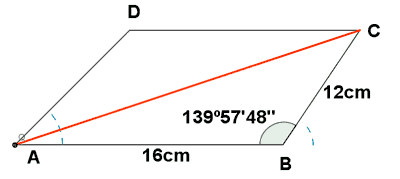
3) Hallar las diagonales de un paralelogramo ABCD cuyo lado AB mide 16 cm y el lado AD mide 12 cm, y el ángulo A = 40o 2' 12''
4) Dos circunferencias cuyos radios son 10 y 12 cm se cortan. El ángulo que forman las tangentes respectivas en el punto de intersección mide 40o. Halla la distancia entre los dos centros de la circunferencia.
5) Dos circunferencias son tangentes exteriores y sus radios miden 8 y 5 m. Halla el ángulo 2α que forman sus tangentes comunes.
6) Las tangentes comunes a dos circunferencias secantes de 2 y 3 cm de radio forman un ángulo de 36o. Calcula la distancia que hay entre los centros de las circunferencias.
7) Un solar tiene forma de triángulo y se conocen dos lados que miden 36 m y 46 m, y el ángulo que forman es de 125o. El metro cuadrado vale 100 €. Calcula el valor del solar.
8) Se quiere calcular la distancia AC entre una casa y un árbol, separados por un río. Para ello nos separamos una distancia AB = 100 m, midiendo los ángulos CAB = 52o y CBA = 42o
9) Para hallar la distancia entre dos puntos inaccesibles C y D (por ejemplo la distancia entre dos barcos, entre los dos picos de una cordillera o entre dos árboles inaccesibles por un rio) fijamos dos puntos A y B tales que AB = 500 m y medimos los siguientes ángulos con el teodolito:
CAD = 50o DAB = 63o ABC = 38o CBD = 57o
Ejercicios resueltos de triángulos cualesquiera I
1) Encuentra la superficie de una parcela que tiene forma de cuadrilátero como la figura, en el que se conocen las siguientes medidas:
a) Lados: AB = 9 m BC = 12 m CD = 6 m AD = 8 m
b) Diagonal: BD = 15 m
Calculamos en primer lugar el área A1 definida por el triángulo ABD:
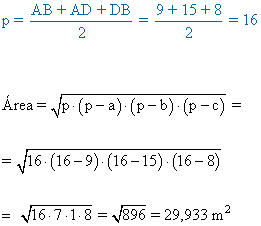
A continuación el área del segundo triángulo, A2 definido por BCD:
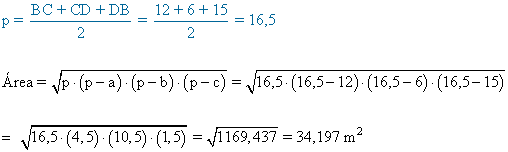
Por lo tanto, el área del cuadrilátero sería:
![]()
2) Calcular los lados de un paralelogramo cuyas diagonales miden 6 cm y 5 cm y el ángulo que forma es de 35o 42' 32''
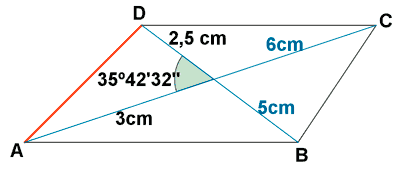
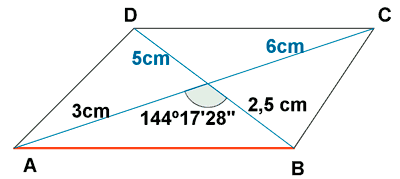
Partimos de la propiedad de que la diagonales de un paralelogramo se cortan por su punto medio:

![]()
3) Hallar las diagonales de un paralelogramo ABCD cuyo lado AB mide 16 cm y el lado AD mide 12 cm, y el ángulo A = 40o 2' 12''
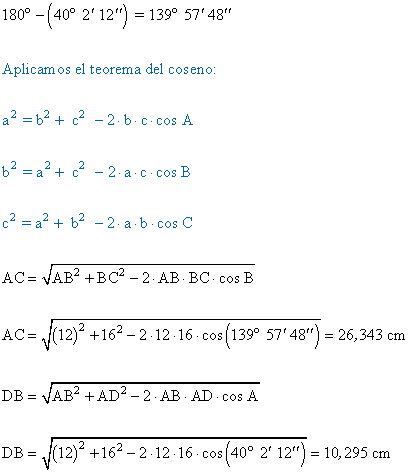
4) Dos circunferencias cuyos radios son 10 y 12 cm se cortan. El ángulo que forman las tangentes respectivas en el punto de intersección mide 40o. Halla la distancia entre los dos centros de la circunferencia.
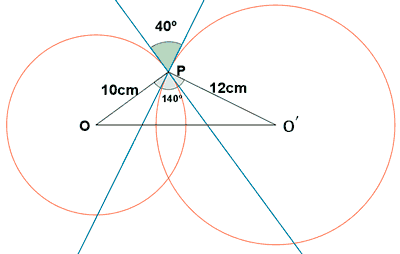
![]()
Aplicando el teorema del coseno en el triángulo OPO' tenemos que:
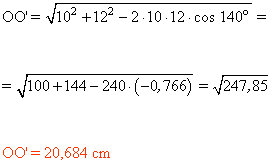
5) Dos circunferencias son tangentes exteriores y sus radios miden 8 y 5 m. Halla el ángulo 2α que forman sus tangentes comunes.
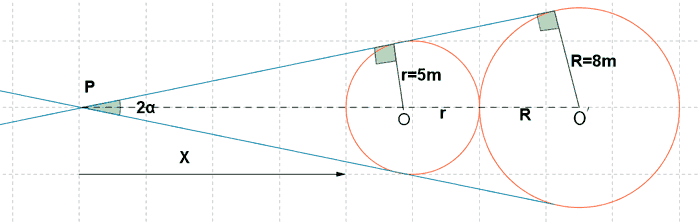
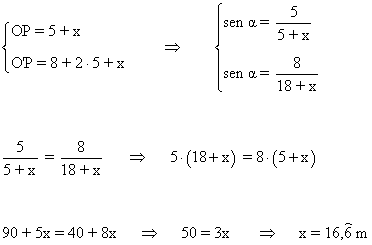
Una vez conocido el valor de x calculamos el ángulo α :
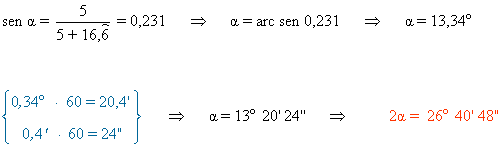
6) Las tangentes comunes a dos circunferencias secantes de 2 y 3 cm de radio forman un ángulo de 36o. Calcula la distancia que hay entre los centros de las circunferencias.
El sistema de ecuaciones resulta de la siguiente forma:
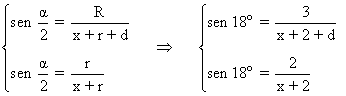
Despejamos la incógnita x de la primera ecuación:
![]()
Sustituimos el valor de x en la primera ecuación:
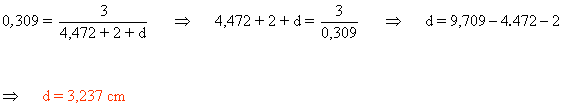
7) Un solar tiene forma de triángulo y se conocen dos lados que miden 36 m y 46 m, y el ángulo que forman es de 125o. El metro cuadrado vale 100 €. Calcula el valor del solar.
Si conocemos dos lados y el ángulo que forman entre ellos podemos calcular el área directamente:
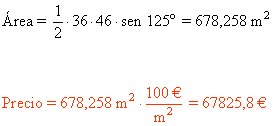
8) Se quiere calcular la distancia AC entre una casa y un árbol, separados por un río. Para ello nos separamos una distancia AB = 100 m, midiendo los ángulos CAB = 52o y CBA = 42o
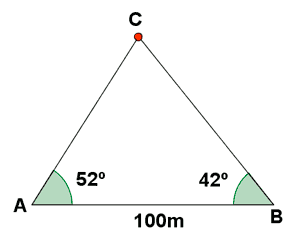
Como los lados de un triángulo suman 180o, tenemos que:
![]()
Calculamos la distancia AC aplicando el teorema del seno:
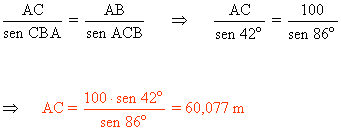
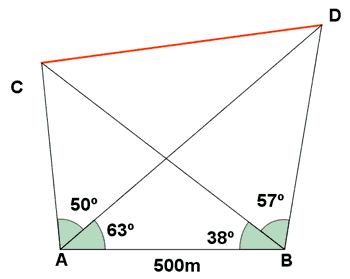
9) Para hallar la distancia entre dos puntos inaccesibles C y D (por ejemplo la distancia entre dos barcos, entre los dos picos de una cordillera o entre dos árboles inaccesibles por un rio) fijamos dos puntos A y B tales que AB = 500 m y medimos los siguientes ángulos con el teodolito:
CAD = 50o DAB = 63o ABC = 38o CBD = 57o
Como los ángulos de un triángulo suman 180o, podemos calcular los ángulos ACB y ADB:
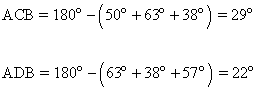
En el triángulo ABC se calcula AC aplicando el teorema del seno:
![]()
Aplicamos también el teorema del seno para calcular el lado AD en el triángulo ABD: seno:
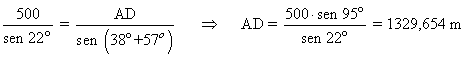
En último lugar mediante el teorema del coseno se calcula el lado CD en el triángulo ACD:
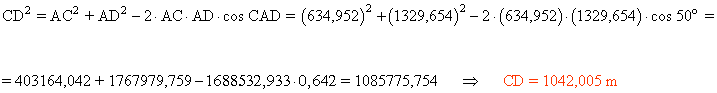


 INICIO
INICIO