Fórmula de Moivre
Aplicando las propiedades de la potencia de un número complejo, se obtiene la siguiente fórmula:
![]()
Dicha fórmula es bastante útil en trigonometría, ya que podemos calcular cos nα y sen nα en función de cos α y sen α .
Ejemplo
1) Calcula la cuarta potencia del número complejo 4 + 4√3 aplicando la fórmula de Moivre:
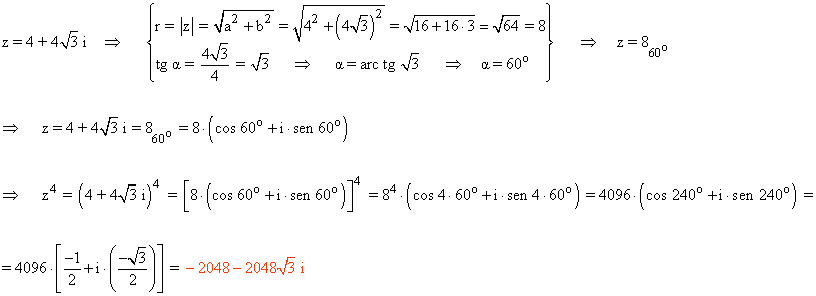
2) Calcula aplicando la fórmula de Moivre: (1 + i)20
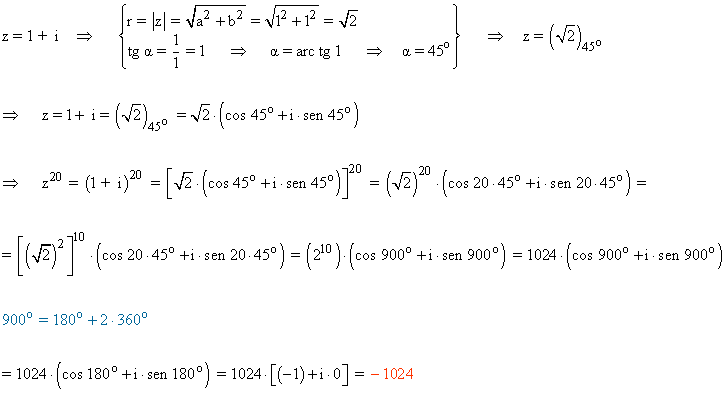
Encuentra la fórmula para calcular sen 2α y cos 2α en función de sen α y cos α.
![]()
Desarrollando el primer miembro por el cuadrado de una suma:
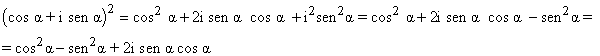
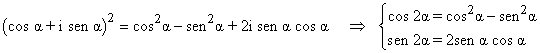
Encuentra la fórmula para calcular sen 3α y cos 3α en función de sen α y cos α.
Aplicando la fórmula de Moivre:
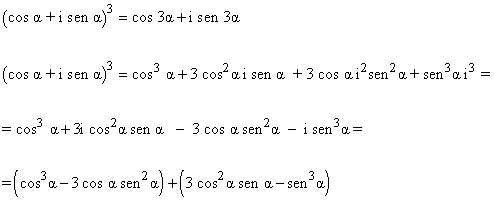
Igualamos el resultado anterior con la segunda parte de la igualdad y separamos en real e imaginario.
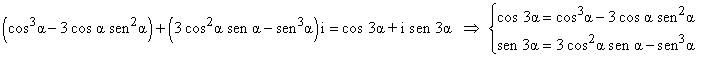


 INICIO
INICIO

